题目内容
如图所示,条形区域Ⅰ和Ⅱ内分别存在方向垂直于纸面向外和向里的匀强磁场,磁感应强度B的大小均为0.3T,AA′、BB′、CC′、DD′为磁场边界,它们相互平行,条形区域的长度足够长,磁场宽度及BB′、CC′之间的距离d=1m.一束带正电的某种粒子从AA′上的O点以沿与AA′成60°角、大小不同的速度射入磁场,当粒子的速度小于某一值v时,粒子在区域Ⅰ内的运动时间t=4×10-6s;当粒子速度为v1时,刚好垂直边界BB′射出区域Ⅰ.取π≈3,不计粒子所受重力. 求:(1)粒子的比荷
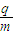 ;
;(2)速度v 和v1的大小;
(3)速度为v1的粒子从O到DD′所用的时间.
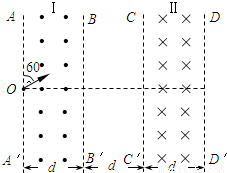
【答案】分析:(1)若粒子的速度小于某一值v时,则粒子不能从BB′离开区域Ⅰ,只能从AA′边离开区域Ⅰ,无论粒子速度大小,在区域Ⅰ中运动的时间相同,作出该粒子的轨迹图,根据几何关系得出圆心角的大小,再根据周期公式得出时间与周期的关系,从而得出粒子的比荷.
(2)当粒子速度为v时,粒子在区域I内的运动轨迹刚好与BB′边界相切,根据几何关系得出粒子运动的半径,再根据粒子在匀强磁场中运动的半径公式求出v 的大小.当粒子速度为v1时,刚好垂直边界BB′射出区域Ⅰ.根据几何关系得出粒子的半径,再根据粒子在匀强磁场中运动的半径公式求出v1 的大小.
(3)速度为v1的粒子在第一个磁场区和第二个磁场区运动的时间相等,根据几何关系求出在磁场区运动的圆心角,从而根据周期公式求出在磁场中运动的时间,粒子在无磁场区做匀速直线运动,根据运动学公式求出在无磁场区运动的时间,从而求出运动的总时间.
解答: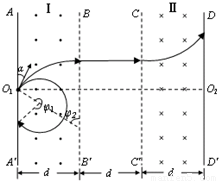 解:(1)若粒子的速度小于某一值v时,则粒子不能从BB′离开区域Ⅰ,只能从AA′边离开区域Ⅰ,无论粒子速度大小,在区域Ⅰ中运动的时间相同,轨迹如图所示(图中只画了一个粒子的轨迹).
解:(1)若粒子的速度小于某一值v时,则粒子不能从BB′离开区域Ⅰ,只能从AA′边离开区域Ⅰ,无论粒子速度大小,在区域Ⅰ中运动的时间相同,轨迹如图所示(图中只画了一个粒子的轨迹).
粒子在区域Ⅰ内做圆周运动的圆心角为φ1=240°,
运动时间: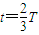
又: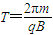
解得: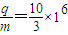 C/kg 或3.3×106C/kg
C/kg 或3.3×106C/kg
(2)当粒子速度为v时,粒子在区域I内的运动轨迹刚好与BB′边界相切,此时有:
R+Rsin30°=d,
又: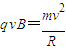
得: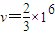 m/s
m/s
当粒子速度为v1时,刚好垂直边界BB′射出区域Ⅰ,
此时轨迹所对圆心角φ2=30,有:R1sinφ2=d
又: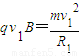
得:v1=2×106m/s
(3)区域I、Ⅱ宽度相同,
则粒子在区域I、Ⅱ中运动时间均为
穿过中间无磁场区域的时间为:
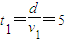 ×10-7s
×10-7s
则粒子从O1到DD′所用的时间:
t= +t1=1.5×10-6s
+t1=1.5×10-6s
答:(1)粒子的比荷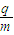 为3.3×106C/kg.
为3.3×106C/kg.
(2)速度v 和v1的大小分别为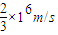 、2×106m/s.
、2×106m/s.
(3)速度为v1的粒子从O到DD′所用的时间为1.5×10-6s.
点评:解决本题的关键作出粒子运动的轨迹图,通过几何关系找出粒子运动的半径以及圆心角的大小,掌握粒子在匀强磁场中运动的半径公式和周期公式.
(2)当粒子速度为v时,粒子在区域I内的运动轨迹刚好与BB′边界相切,根据几何关系得出粒子运动的半径,再根据粒子在匀强磁场中运动的半径公式求出v 的大小.当粒子速度为v1时,刚好垂直边界BB′射出区域Ⅰ.根据几何关系得出粒子的半径,再根据粒子在匀强磁场中运动的半径公式求出v1 的大小.
(3)速度为v1的粒子在第一个磁场区和第二个磁场区运动的时间相等,根据几何关系求出在磁场区运动的圆心角,从而根据周期公式求出在磁场中运动的时间,粒子在无磁场区做匀速直线运动,根据运动学公式求出在无磁场区运动的时间,从而求出运动的总时间.
解答:
 解:(1)若粒子的速度小于某一值v时,则粒子不能从BB′离开区域Ⅰ,只能从AA′边离开区域Ⅰ,无论粒子速度大小,在区域Ⅰ中运动的时间相同,轨迹如图所示(图中只画了一个粒子的轨迹).
解:(1)若粒子的速度小于某一值v时,则粒子不能从BB′离开区域Ⅰ,只能从AA′边离开区域Ⅰ,无论粒子速度大小,在区域Ⅰ中运动的时间相同,轨迹如图所示(图中只画了一个粒子的轨迹).粒子在区域Ⅰ内做圆周运动的圆心角为φ1=240°,
运动时间:
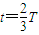
又:
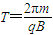
解得:
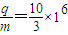 C/kg 或3.3×106C/kg
C/kg 或3.3×106C/kg (2)当粒子速度为v时,粒子在区域I内的运动轨迹刚好与BB′边界相切,此时有:
R+Rsin30°=d,
又:
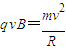
得:
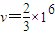 m/s
m/s 当粒子速度为v1时,刚好垂直边界BB′射出区域Ⅰ,
此时轨迹所对圆心角φ2=30,有:R1sinφ2=d
又:
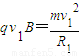
得:v1=2×106m/s
(3)区域I、Ⅱ宽度相同,
则粒子在区域I、Ⅱ中运动时间均为

穿过中间无磁场区域的时间为:
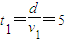 ×10-7s
×10-7s 则粒子从O1到DD′所用的时间:
t=
 +t1=1.5×10-6s
+t1=1.5×10-6s答:(1)粒子的比荷
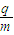 为3.3×106C/kg.
为3.3×106C/kg.(2)速度v 和v1的大小分别为
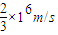 、2×106m/s.
、2×106m/s.(3)速度为v1的粒子从O到DD′所用的时间为1.5×10-6s.
点评:解决本题的关键作出粒子运动的轨迹图,通过几何关系找出粒子运动的半径以及圆心角的大小,掌握粒子在匀强磁场中运动的半径公式和周期公式.

练习册系列答案
相关题目
 (2011?江苏一模)如图所示,条形区域Ⅰ和Ⅱ内分别存在方向垂直于纸面向外和向里的匀强磁场,磁感应强度B的大小均为0.3T,AA′、BB′、CC′、DD′为磁场边界,它们相互平行,条形区域的长度足够长,磁场宽度及BB′、CC′之间的距离d=1m.一束带正电的某种粒子从AA′上的O点以沿与AA′成60°角、大小不同的速度射入磁场,当粒子的速度小于某一值v0时,粒子在区域Ⅰ内的运动时间t0=4×10-6s;当粒子速度为v1时,刚好垂直边界BB′射出区域Ⅰ.取π≈3,不计粒子所受重力. 求:
(2011?江苏一模)如图所示,条形区域Ⅰ和Ⅱ内分别存在方向垂直于纸面向外和向里的匀强磁场,磁感应强度B的大小均为0.3T,AA′、BB′、CC′、DD′为磁场边界,它们相互平行,条形区域的长度足够长,磁场宽度及BB′、CC′之间的距离d=1m.一束带正电的某种粒子从AA′上的O点以沿与AA′成60°角、大小不同的速度射入磁场,当粒子的速度小于某一值v0时,粒子在区域Ⅰ内的运动时间t0=4×10-6s;当粒子速度为v1时,刚好垂直边界BB′射出区域Ⅰ.取π≈3,不计粒子所受重力. 求: 如图所示,条形区域AA′BB′中存在方向垂直于纸面向外的匀强磁场,磁感应强度B的大小为0.3T,AA′、BB′为磁场边界,它们相互平行,条形区域的长度足够长,宽度d=1m.一束带正电的某种粒子从AA′上的O点以沿着与AA′成60°角、大小不同的速度射入磁场,当粒子的速度小于某一值v0时,粒子在磁场区域内的运动时间t0=4×10-6s;当粒子速度为v1时,刚好垂直边界BB′射出磁场.取π=3,不计粒子所受重力.求:
如图所示,条形区域AA′BB′中存在方向垂直于纸面向外的匀强磁场,磁感应强度B的大小为0.3T,AA′、BB′为磁场边界,它们相互平行,条形区域的长度足够长,宽度d=1m.一束带正电的某种粒子从AA′上的O点以沿着与AA′成60°角、大小不同的速度射入磁场,当粒子的速度小于某一值v0时,粒子在磁场区域内的运动时间t0=4×10-6s;当粒子速度为v1时,刚好垂直边界BB′射出磁场.取π=3,不计粒子所受重力.求:
 ;
;