��Ŀ����
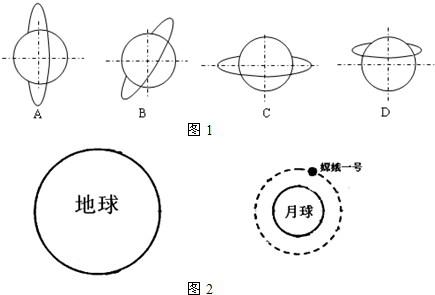
�ҹ�����ġ��϶�һ�š����Ǿ�����μ��١��������ճɹ����뻷�¹����������ͼ��ʾ�����Ǽȿ�����������ȽϽ���Բ���a���˶���Ҳ������������Ƚ�Զ��Բ���b���˶�������˵����ȷ���ǣ�������

| A��������a�����е����ٶ�С����b�����е����ٶ� |
| B��������a�����е����ڴ�����b�����е����� |
| C��������a�����еĽ��ٶ�С����b�����еĽ��ٶ� |
| D��������a������ʱ�ܵ�����������������b������ʱ���������� |

������������ǣ����������ṩ�������������ǵ�����Ϊm������뾶Ϊr����������ΪM����
F=F��
F=
F��=m
=m��2r=m
���
v=
��=
T=2��
��������ã�������a�����еĹ���뾶С����b�����еĹ���뾶��
����������a�����е����ٶȴ��ٶȴ�����С������������A��B��C����D��ȷ��
��ѡD��
F=F��
F=
| GMm |
| r2 |
F��=m
| v2 |
| r |
| 4��2r |
| T2 |
���
v=
|
��=
|
T=2��
|
��������ã�������a�����еĹ���뾶С����b�����еĹ���뾶��
����������a�����е����ٶȴ��ٶȴ�����С������������A��B��C����D��ȷ��
��ѡD��

��ϰ��ϵ�д�
�����Ŀ
 �ҹ�����ġ��϶�һ�š�����������һ�������У�����˼ȶ�������2009��3��1��16ʱ13�ֳɹ�ײ�£���ͼΪ���϶�һ�š�����ײ�µ�ģ��ͼ�������ڿ��Ƶ�1��ʼ����ײ�¹��������������������Բ���˶��Ĺ���뾶ΪR������ΪT����������ΪG������������Ϣ������˵����ȷ���ǣ���������
�ҹ�����ġ��϶�һ�š�����������һ�������У�����˼ȶ�������2009��3��1��16ʱ13�ֳɹ�ײ�£���ͼΪ���϶�һ�š�����ײ�µ�ģ��ͼ�������ڿ��Ƶ�1��ʼ����ײ�¹��������������������Բ���˶��Ĺ���뾶ΪR������ΪT����������ΪG������������Ϣ������˵����ȷ���ǣ��������� �ҹ�����ġ��϶�һ�š����Ǿ�����μ��١��������ճɹ����뻷�¹����������ͼ��ʾ�����Ǽȿ�����������ȽϽ���Բ���a���˶���Ҳ������������Ƚ�Զ��Բ���b���˶�������˵����ȷ���ǣ�������
�ҹ�����ġ��϶�һ�š����Ǿ�����μ��١��������ճɹ����뻷�¹����������ͼ��ʾ�����Ǽȿ�����������ȽϽ���Բ���a���˶���Ҳ������������Ƚ�Զ��Բ���b���˶�������˵����ȷ���ǣ������� ��2008?�Ϻ�ģ�⣩�ҹ�����ġ��϶�һ�š�̽�����Ǽ��·��ʾ��ͼ��ͼ��ʾ�������ɵ��淢������ͣ���������ͣ��������ٺ�������ת�ƹ�����ٴε��ٺ���빤����������ǿ�ʼ���������̽�⣮��֪���������������֮��Ϊa��������Ե����ͣ��������������������Ĺ�������İ뾶֮��Ϊb��������ͣ�������������Ͼ�����Ϊ����Բ���˶�����������ͣ��������������������֮��Ϊ
��2008?�Ϻ�ģ�⣩�ҹ�����ġ��϶�һ�š�̽�����Ǽ��·��ʾ��ͼ��ͼ��ʾ�������ɵ��淢������ͣ���������ͣ��������ٺ�������ת�ƹ�����ٴε��ٺ���빤����������ǿ�ʼ���������̽�⣮��֪���������������֮��Ϊa��������Ե����ͣ��������������������Ĺ�������İ뾶֮��Ϊb��������ͣ�������������Ͼ�����Ϊ����Բ���˶�����������ͣ��������������������֮��Ϊ 2010��10��1��18��59��57�룬�ҹ����������Ƿ���վ�����ˡ��϶���š������ҹ�����ġ��϶�һ�š����������������ȶ����У�������˼ȶ������϶���š��롰�϶�һ�š������ͬ���ڡ��϶���š������������˴��������ֱ�ӱ��͵�����ת�ƹ���������϶�һ�š����ͳ�����������������䣮��ͼ��ʾ��Ϊ���϶�һ�š��ڵ���ת�ƵĹ����һ���֣���P��Q�˶���ֱ��MN�ǹ�O���Һ����߹켣���У�����˵��������ǣ�������
2010��10��1��18��59��57�룬�ҹ����������Ƿ���վ�����ˡ��϶���š������ҹ�����ġ��϶�һ�š����������������ȶ����У�������˼ȶ������϶���š��롰�϶�һ�š������ͬ���ڡ��϶���š������������˴��������ֱ�ӱ��͵�����ת�ƹ���������϶�һ�š����ͳ�����������������䣮��ͼ��ʾ��Ϊ���϶�һ�š��ڵ���ת�ƵĹ����һ���֣���P��Q�˶���ֱ��MN�ǹ�O���Һ����߹켣���У�����˵��������ǣ�������