题目内容
15.2014年世界一级方程式锦标赛,在某一赛场长直的赛道上有一辆F1赛车,前方187.5m处有一辆服务车正以10m/s的速度匀速前进,这时赛车从静止出发4m/s2的加速度追赶;试求:(1)赛车何时追上服务车?
(2)追上之前与服务车有最远距离,还是最近距离?是多少?
(3)当赛车刚追上服务车时,赛车手立即刹车,从赛车开始运动到赛车停止的时间内,两车能否第二次相遇?说明理由.
分析 (1)根据位移关系,结合运动学公式求出追及的时间.
(2)当两车速度相等时,有最远距离,结合速度公式和位移公式求出最远距离.
(3)通过赛车刹车到停止过程中的平均速度与服务车的速度比较,判断能否发生第二次相遇.
解答 解:(1)设经过时间t赛车能追上服务车,由位移关系可得:$\frac{1}{2}a{t}_{\;}^{2}=vt+187.5$,
代入数据解得:t=12.5s.
(2)当两车速度相等时,之间的距离最远,即:v=at′,
代入数据解得:t′=2.5s,
两者之间的最大位移为:${s}_{max}^{\;}={v}_{0}^{\;}t′+187.5-\frac{1}{2}at{′}_{\;}^{2}$,
代入数据解得:smax=200m.
(3)从赛车开始刹车到赛车停止,这一过程中的平均速度为:$\overline{v}=\frac{at+0}{2}=\frac{12.5×4+0}{2}=25m/s$,显然大于服务车的速度10m/s,故不可能第二次相遇.
答:(1)赛车经过12.5s追上服务车.
(2)追上之前有最大距离,为200m.
(3)不能发生第二次相遇.
点评 本题考查了运动学中追及问题,关键抓住位移关系,结合运动学公式进行求解,知道速度相等时,两车有最远距离.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知做匀加速直线运动的物体在第5s末速度为10m/s,则物体( )
| A. | 加速度一定为2 m/s2 | B. | 前5 s内位移不可能是25 m | ||
| C. | 前10 s内位移一定为100 m | D. | 前10 s内位移不一定为100 m |
6.两个做匀加速直线运动的物体都运动了t秒,下列说法正确的是( )
| A. | 加速度大的物体,通过的位移一定大 | |
| B. | 初速度大的物体,通过的位移一定大 | |
| C. | 末速度大的物体,通过的位移一定大 | |
| D. | 平均速度大的物体,通过的位移一定大 |
3. 利用如图所示的试验装置可以测量磁场的磁感应强度的大小;用绝缘轻质细线把底边长为L、电阻为R、质量为m的U形线框竖直悬挂在力敏传感器的挂钩上,将线框置于待测磁场中(可视为匀强磁场),线框平面与磁场方向垂直,用轻质导线在连接线框与直流电源,电源电阻不计,电动势可调,导线的电阻忽略不计;当外界拉力F作用于力敏传感器的挂钩上时,力敏传感器会显示拉力的大小为F;当线框接电动势为E1时,力敏传感器显示拉力的大小为F1; 当线框接电动势为E2时,力敏传感器显示拉力的大小为F2;下列说法正确的是( )
利用如图所示的试验装置可以测量磁场的磁感应强度的大小;用绝缘轻质细线把底边长为L、电阻为R、质量为m的U形线框竖直悬挂在力敏传感器的挂钩上,将线框置于待测磁场中(可视为匀强磁场),线框平面与磁场方向垂直,用轻质导线在连接线框与直流电源,电源电阻不计,电动势可调,导线的电阻忽略不计;当外界拉力F作用于力敏传感器的挂钩上时,力敏传感器会显示拉力的大小为F;当线框接电动势为E1时,力敏传感器显示拉力的大小为F1; 当线框接电动势为E2时,力敏传感器显示拉力的大小为F2;下列说法正确的是( )
 利用如图所示的试验装置可以测量磁场的磁感应强度的大小;用绝缘轻质细线把底边长为L、电阻为R、质量为m的U形线框竖直悬挂在力敏传感器的挂钩上,将线框置于待测磁场中(可视为匀强磁场),线框平面与磁场方向垂直,用轻质导线在连接线框与直流电源,电源电阻不计,电动势可调,导线的电阻忽略不计;当外界拉力F作用于力敏传感器的挂钩上时,力敏传感器会显示拉力的大小为F;当线框接电动势为E1时,力敏传感器显示拉力的大小为F1; 当线框接电动势为E2时,力敏传感器显示拉力的大小为F2;下列说法正确的是( )
利用如图所示的试验装置可以测量磁场的磁感应强度的大小;用绝缘轻质细线把底边长为L、电阻为R、质量为m的U形线框竖直悬挂在力敏传感器的挂钩上,将线框置于待测磁场中(可视为匀强磁场),线框平面与磁场方向垂直,用轻质导线在连接线框与直流电源,电源电阻不计,电动势可调,导线的电阻忽略不计;当外界拉力F作用于力敏传感器的挂钩上时,力敏传感器会显示拉力的大小为F;当线框接电动势为E1时,力敏传感器显示拉力的大小为F1; 当线框接电动势为E2时,力敏传感器显示拉力的大小为F2;下列说法正确的是( )| A. | 当线框接电动势为E1的电源时所受安培力的大小为F1 | |
| B. | 当线框接电动势为E2的电源时力敏传感器显示的拉力大小为线框所受安培力大小与重力大小之差 | |
| C. | 待测磁场的磁感应强度为$\frac{({F}_{1}-{F}_{2})R}{({E}_{2}-{E}_{1}^{\;})L}$ | |
| D. | 待测磁场的磁感应强度为$\frac{({F}_{1}-{F}_{2})R}{({E}_{1}-{E}_{2})L}$ |
10.某人在t=0时刻开始观察一个正在做匀加速直线运动的质点,现只测出了该质点在第3秒内和第7秒内的位移,则下列说法正确的是( )
| A. | 能求出质点的初速度 | B. | 能求出质点的加速度 | ||
| C. | 能求出质点任意时刻的瞬时速度 | D. | 不能求出7秒内的总位移 |
20. 乐乐同学想利用“电磁弹簧秤”称量一金属棒的质量,如图所示,一根粗细均匀的金属棒ab用两个完全相同的弹簧悬挂在匀强磁场中,碰场的磁感应强度方向垂直于纸面向里,弹簧上端固定,下端与金属棒连接且绝缘,金属棒通过开关与一电路相连,电源右侧为正极,开关接通以后,下列说法正确的是( )
乐乐同学想利用“电磁弹簧秤”称量一金属棒的质量,如图所示,一根粗细均匀的金属棒ab用两个完全相同的弹簧悬挂在匀强磁场中,碰场的磁感应强度方向垂直于纸面向里,弹簧上端固定,下端与金属棒连接且绝缘,金属棒通过开关与一电路相连,电源右侧为正极,开关接通以后,下列说法正确的是( )
 乐乐同学想利用“电磁弹簧秤”称量一金属棒的质量,如图所示,一根粗细均匀的金属棒ab用两个完全相同的弹簧悬挂在匀强磁场中,碰场的磁感应强度方向垂直于纸面向里,弹簧上端固定,下端与金属棒连接且绝缘,金属棒通过开关与一电路相连,电源右侧为正极,开关接通以后,下列说法正确的是( )
乐乐同学想利用“电磁弹簧秤”称量一金属棒的质量,如图所示,一根粗细均匀的金属棒ab用两个完全相同的弹簧悬挂在匀强磁场中,碰场的磁感应强度方向垂直于纸面向里,弹簧上端固定,下端与金属棒连接且绝缘,金属棒通过开关与一电路相连,电源右侧为正极,开关接通以后,下列说法正确的是( )| A. | 金属棒所受安培力竖直向下 | |
| B. | 仅改变电流方向,安培力方向不变 | |
| C. | 仅增大磁感应强度,安培力变小 | |
| D. | 若滑动变阻器的滑片向左滑动,则安培力减小 |
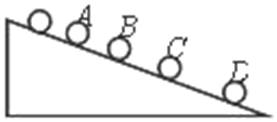 从斜面上某位置,每隔0.1s由静止开始释放一个小球,在连续释放几个后,对在斜面上的小球拍下照片,如图所示,测得sAB=15cm,sBC=20cm,试求:
从斜面上某位置,每隔0.1s由静止开始释放一个小球,在连续释放几个后,对在斜面上的小球拍下照片,如图所示,测得sAB=15cm,sBC=20cm,试求: “验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.
“验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.