题目内容
15. 如图所示,一边长为L,质量为m,电阻为R的正方形金属框放置在倾角为θ的光滑的绝缘斜面上,磁场的方向垂直金属矿平面,磁感应强度的大小只随y的方向变化,规律为B=B0+ky,k为恒定的大于零的常数.在斜面内以平行于x轴的水平初速度O点抛出金属矿,运动一段时间后金属矿的速度恒定为v,假设运动过程中金属框总有两条边与y轴平行,且金属框不转动,当金属框沿y轴方向运动距离为h时速度达到最大.不计空气阻力,斜面和磁场区域足够大,重力加速度为g
如图所示,一边长为L,质量为m,电阻为R的正方形金属框放置在倾角为θ的光滑的绝缘斜面上,磁场的方向垂直金属矿平面,磁感应强度的大小只随y的方向变化,规律为B=B0+ky,k为恒定的大于零的常数.在斜面内以平行于x轴的水平初速度O点抛出金属矿,运动一段时间后金属矿的速度恒定为v,假设运动过程中金属框总有两条边与y轴平行,且金属框不转动,当金属框沿y轴方向运动距离为h时速度达到最大.不计空气阻力,斜面和磁场区域足够大,重力加速度为g(1)试求水平速度v0的大小;
(2)求金属矿从开始运动到达恒定速度v后,沿y轴方向位移为s时,金属框中产生的内能多大.
分析 在x方向磁场没有不会,所以沿x轴方向,两边产生感应电动势合为0,安培力为0.
在y方向,上产生感应电动之和为E=(B0+k(y+L))Lvy-(B0+ky)Lvy=kL2vy,然后根据欧姆定律和力与平衡列式求解Vy,然后根据速度的分解求解初速度v0;
根据能量守恒定律求产生热量Q.
解答 解:(1)在x方向磁场没有不会,所以沿x轴方向,两边产生感应电动势合为0,安培力为0,故x方向线框做匀速直线运动;在y方向,上产生感应电动之和为E=(B0+k(y+L))Lvy-(B0+ky)Lvy=kL2vy,稳定时安培力等于重力的分力
即BIL=mgsinθ=B•$\frac{k{L}^{2}{v}_{y}}{R}$L
解得vy=$\frac{mgRsinθ}{k{BL}^{3}}$
根据运动的合成与分解知v0=$\sqrt{{v}^{2}-{v}_{y}^{2}}$=$\sqrt{{v}^{2}-\frac{{m}^{2}{g}^{2}{R}^{2}si{n}^{2}θ}{{k}^{2}{B}^{2}{L}^{6}}}$
(2)根据能量守恒定律知产生热量Q=mgssinθ$-\frac{1}{2}m{v}_{y}^{2}$=mgssinθ-$\frac{1}{2}×$m×$(\frac{mgRsinθ}{kB{L}^{3}})^{2}$=mgssinθ-$\frac{{m}^{3}{g}^{2}{R}^{2}si{n}^{2}θ}{2{k}^{2}{B}^{2}{L}^{6}}$
答:(1)水平速度v0的大小为$\sqrt{{v}^{2}-\frac{{m}^{2}{g}^{2}{R}^{2}si{n}^{2}θ}{{k}^{2}{B}^{2}{L}^{6}}}$;
(2)金属矿从开始运动到达恒定速度v后,沿y轴方向位移为s时,金属框中产生的内能为mgssinθ-$\frac{{m}^{3}{g}^{2}{R}^{2}si{n}^{2}θ}{2{k}^{2}{B}^{2}{L}^{6}}$.
点评 此题考查电磁感应和类平抛运动的综合应用,同时涉及到能量,要注意利用能量守恒求解会比较简单.

 名校课堂系列答案
名校课堂系列答案 如图所示,A、B、C、D为四个物体,K1、K2为两个轻弹簧,E为跨过光滑定滑轮的轻绳.物体A在水平地面上,定滑轮左右两段轻绳都处于竖直状态,它们的连接如图所示并都处于静止状态.下列说法正确的是( )
如图所示,A、B、C、D为四个物体,K1、K2为两个轻弹簧,E为跨过光滑定滑轮的轻绳.物体A在水平地面上,定滑轮左右两段轻绳都处于竖直状态,它们的连接如图所示并都处于静止状态.下列说法正确的是( )| A. | K1、K2一定都处于拉伸状态 | |
| B. | K1、K2一定都处于压缩状态 | |
| C. | 有可能K1处于拉伸状态,K2处于压缩状态 | |
| D. | 有可能K1处于压缩状态,K2处于拉伸状态 |
| A. | 甲、乙在空中运动的时间相等 | B. | 甲落地后,经1s乙还在空中运动 | ||
| C. | 甲、乙间的速度差与时间成正比 | D. | 甲、乙下落的加速度一样大 |
 一列简谐横波沿x轴正向传播,O、A、B、C、D为传播方向上的五个质点,相邻质点之间相隔1.0m,如图所示.t=0时刻波源O点开始向y轴正方向运动.经过0.10s它第一次达到正向最大位移,而此时刻B质点开始从平衡位置开始向y轴正方向运动.由此可以确定( )
一列简谐横波沿x轴正向传播,O、A、B、C、D为传播方向上的五个质点,相邻质点之间相隔1.0m,如图所示.t=0时刻波源O点开始向y轴正方向运动.经过0.10s它第一次达到正向最大位移,而此时刻B质点开始从平衡位置开始向y轴正方向运动.由此可以确定( )| A. | 这列波的波长为8.0m | |
| B. | 周期为1.0s | |
| C. | 这列波的波速为20m/s,频率是2.5Hz | |
| D. | 在0.30s末D质点刚开始振动 | |
| E. | 在0.30s末D质点第一次达到正向最大位移 |
| A. | 用活塞封闭在气缸中的一定量的气体,外界对其做功,其内能可能减少,但其压强一定增大 | |
| B. | 用活塞封闭在气缸中的一定量的气体,温度升高时,气体分子热运动的平运动能增大,其压强也一定增大 | |
| C. | 一定量气体的内能等于其所有分子热运动动能和分子势能的总和 | |
| D. | 可以制作一个装置从海水中吸收内能全部用来做功而不产生其它影响 |
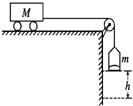 如图,把小车放在光滑的水平桌面上,用轻绳跨过定滑轮使之与盛有沙子的小桶相连,已知小车的质量为M,小桶与沙子的总质量为m,把小车从静止状态释放后,在小桶下落竖直高度为h的过程中,若不计滑轮及空气的阻力,下列说法正确的是( )
如图,把小车放在光滑的水平桌面上,用轻绳跨过定滑轮使之与盛有沙子的小桶相连,已知小车的质量为M,小桶与沙子的总质量为m,把小车从静止状态释放后,在小桶下落竖直高度为h的过程中,若不计滑轮及空气的阻力,下列说法正确的是( )| A. | 绳拉车的力始终为mg | |
| B. | 当M远远大于m时,才可以认为绳拉车的力为mg | |
| C. | 小车获得的动能为$\frac{Mmgh}{M+m}$ | |
| D. | 小车获得的动能为mgh |
 如图所示,放在水平地面上的光滑绝缘筒有两个带正电的小球A、B,A位于筒底靠左侧壁处,B在右侧筒壁上P处时处于平衡状态,现将B小球向上移动一段距离,从E处由静止开始释放,则在它下落到筒底前( )
如图所示,放在水平地面上的光滑绝缘筒有两个带正电的小球A、B,A位于筒底靠左侧壁处,B在右侧筒壁上P处时处于平衡状态,现将B小球向上移动一段距离,从E处由静止开始释放,则在它下落到筒底前( )| A. | 小球A对筒底的压力保持不变 | B. | 小球B对筒壁的压力逐渐增大 | ||
| C. | 小球B的动能先增大后减小 | D. | 小球A、B间的电势能逐渐减小 |
 如图所示,竖直放置的光滑圆环,半径为R=0.4m,质量为m=0.4kg小球沿环内侧做完整的圆周运动(如过山车),取g=10m/s2,求:
如图所示,竖直放置的光滑圆环,半径为R=0.4m,质量为m=0.4kg小球沿环内侧做完整的圆周运动(如过山车),取g=10m/s2,求: 如图所示,M、N为两块水平放置的平行金属板,长为L,相距为2d,当S断开时(两板未充电),一带电量为+q,质量为m的油滴,以一水平初速度从两板间中点p飞入,恰好落到下板的中点Q处.求:
如图所示,M、N为两块水平放置的平行金属板,长为L,相距为2d,当S断开时(两板未充电),一带电量为+q,质量为m的油滴,以一水平初速度从两板间中点p飞入,恰好落到下板的中点Q处.求: