题目内容
如图所示，以ab为边界的两匀强磁场的磁感应强度为B1=2B，B2=B，现有一质量为m、带电荷量为+q的粒子从0点以初速度．沿垂直于ab方向发射．在图中作出粒子的运动轨迹，并求出粒子发射后第7次穿过直线ab时所经历的时间、路程及离开点0的距离．（粒子重力不计）分析：粒子在两种磁场中只受洛伦兹力，做匀速圆周运动，根据牛顿第二定律可知半径之比为1：2，根据左手定则，分析粒子旋转方向，画出轨迹．根据轨迹，确定时间与周期的关系，根据半径公式求出离开点0的距离以及通过周期公式求出经历的时间．
解答：
解：设粒子在磁场B1和B2中圆周运动的半径分别为r1、r2
则r1=
，r2=
由题B1=2B2，得r1：r2=1：2
根据左手定则判断可知，粒子在磁场B1中沿逆时针方向旋转，在磁场B2中沿顺时针方向旋转．则轨迹如图．
根据几何关系知，第7次通过直线ab时，在上面磁场形成四个小半圆，在下面磁场形成三个大半圆．
则经历的时间为：t=2T1+
T2=2?
+
?
=
．
离开O点的距离为：x=4r1=4×
=
．
经历的路程为：s=2×2πr1+
×2πr2=
．
答：轨迹如图所示，粒子发射后第7次穿过直线ab时所经历的时间为
，路程为
，距离O点的距离为
．
解：设粒子在磁场B1和B2中圆周运动的半径分别为r1、r2则r1=
| mv |
| qB1 |
| mv |
| qB 2 |
由题B1=2B2，得r1：r2=1：2
根据左手定则判断可知，粒子在磁场B1中沿逆时针方向旋转，在磁场B2中沿顺时针方向旋转．则轨迹如图．
根据几何关系知，第7次通过直线ab时，在上面磁场形成四个小半圆，在下面磁场形成三个大半圆．
则经历的时间为：t=2T1+
| 3 |
| 2 |
| 2πm |
| q?2B |
| 3 |
| 2 |
| 2πm |
| qB |
| 5πm |
| qB |
离开O点的距离为：x=4r1=4×
| mv |
| q?2B |
| 2mv |
| qB |
经历的路程为：s=2×2πr1+
| 3 |
| 2 |
| 5πmv |
| qB |
答：轨迹如图所示，粒子发射后第7次穿过直线ab时所经历的时间为
| 5πm |
| qB |
| 5πmv |
| qB |
| 2mv |
| qB |
点评：本题重点考查作图能力．带电粒子在磁场中运动问题，画轨迹是解决这类问题的关键．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
（2012?石家庄一模）在倾角为θ足够长的光滑斜面上，存在着两个磁感应强度相等的匀强磁场，磁场方向一个垂直斜面向上，另一个垂直斜面向下，宽度均为L，如图所示．一个质量为m、电阻为R、边长也为L的正方形线框在t=0时刻以速度v0进入磁场，恰好做匀速直线运动．若经过时间t0，线框ab边到达gg′与ff′中间位置时，线框又恰好做匀速运动，则下列说法正确的是（ ）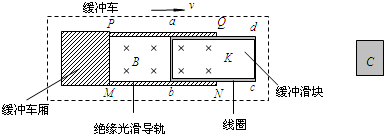
如图所示，在倾角为θ的光滑斜面上，存在着两个磁感应强度大小均为B的匀强磁场，区域I的磁场方向垂直斜面向上，区域Ⅱ的磁场方向垂直斜面向下，磁场的宽度均为L．一个质量为m、电阻为R、边长也为L的正方形导线框，在零时刻由静止开始沿斜面下滑．t1时ab边刚越过GH进入磁场I区，此时线框恰好以速度v1做匀速直线运动；t2时ab边下滑到．JP与MN的中间位置，此时线框又恰好以速度v2做匀速直线运动．重力加速度为g．则下列说法中正确的有（ ）
如图所示，板间距为d、板长为L的两块平行金属板EF、GH 水平放置，在紧靠平行板右侧的正三角形区域内存在着垂直纸面的匀强磁场，三角形底边BC与GH在同一水平线上，顶点A 与EF在同一水平线上．一个质量为m、电量为-q的粒子沿两板中心线以初速度v0水平射入，若在两板之间加某一恒定电压，粒子离开电场后垂直AB 边从D点进入磁场，BD=1/4AB，并垂直AC边射出（不计粒子的重力），求：