题目内容
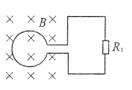
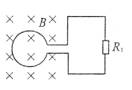
圆形线圈处于磁感应强度为B的匀强磁场中,磁场的方向垂直于线圈平面,线圈半径为r,电阻为R,若用时间Δt把线圈从磁场中拉出来和原地使线圈翻转180°,则通过线圈导线截面的电量分别为__________和__________.
答案:
解析:
提示:
解析:
解题方法:程序法.本题先按法拉第电磁感应定律的应用程序求平均电动势,再用闭合电路欧姆定律求平均电流,最后应用q= 应用法拉第电磁感应定律的程序: (1)确定研究对象.确定产生感应电动势的回路. (2)弄清回路中磁通量的变化ΔΦ,以及发生ΔΦ用的时间Δt. (3)应用定律求电动势.注意线圈的匝数. 解析:匀速拉出时:q= = 原地翻转180°时,磁通量变化 |ΔΦ′|=2BS=2Bπr2, q= |
提示:
点评:(1)计算电量必须用平均感应电流和平均感应电动势.平均感应电动势一般用法拉第电磁感应定律求.(2)若线圈分正、反两面,开始磁感线从正面穿入,磁通量为正,则Φ1=Bπr2;翻转180°时,磁感线从反面穿入,则磁通量为负,Φ2=-Bπr2,翻转180°时磁通量的变化量ΔΦ=Φ2-Φ1=-Bπr2-πBr2=-2Bπr2. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,面积为0.2m2的圆形线圈处于匀强磁场中,磁场方向垂直于线圈平面,已知磁感应强度B随时间变化规律为B=2+0.2t(T),定值电阻R1=6Ω,R2=4Ω,线圈电阻忽略不计,试求:
如图所示,面积为0.2m2的圆形线圈处于匀强磁场中,磁场方向垂直于线圈平面,已知磁感应强度B随时间变化规律为B=2+0.2t(T),定值电阻R1=6Ω,R2=4Ω,线圈电阻忽略不计,试求: