题目内容
半径为R的光滑圆环轨道竖直放置，一质量为m的小球恰能在此圆轨道内做圆周运动，则小球在轨道最低点处对轨道的压力大小为（ ）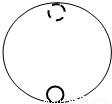
A．3mg
B．4mg
C．5mg
D．6mg
【答案】分析：小球通过轨道最高点时恰好与轨道间没有相互作用力，故由重力提供向心力，根据圆周运动向心力公式即可得出最高点的速度；可以根据机械能守恒定律求出最低点的速度；在最低点由支持力和重力的合力提供向心力，根据圆周运动向心力公式即可求得支持力的大小；最后根据牛顿第三定律得到压力．
解答：解：设小球通过轨道最高点时速度的大小为v1，根据题意和圆周运动向心力公式得：
mg=m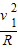
解得：v1=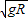
设小球通过轨道最低点的速度大小为v2，从最高点到最低点的过程中运用机械能守恒定律，得：
2mgR=
mv22-
mv12 ①
解得：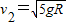
设小球通过轨道最低点时受到轨道支持力大小为FN，根据圆周运动向心力公式得：
FN-mg=m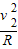
②
由①②解得：FN=6mg
根据牛顿第三定律，球对轨道的压力为6mg；
故选D．
点评：该题是机械能守恒定律及圆周运动向心力公式的直接应用，要抓住恰好到达最高点的隐含条件是由重力来提供向心力，不难．
解答：解：设小球通过轨道最高点时速度的大小为v1，根据题意和圆周运动向心力公式得：
mg=m
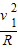
解得：v1=
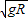
设小球通过轨道最低点的速度大小为v2，从最高点到最低点的过程中运用机械能守恒定律，得：
2mgR=
mv22-mv12 ①解得：
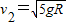
设小球通过轨道最低点时受到轨道支持力大小为FN，根据圆周运动向心力公式得：
FN-mg=m
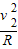②由①②解得：FN=6mg
根据牛顿第三定律，球对轨道的压力为6mg；
故选D．
点评：该题是机械能守恒定律及圆周运动向心力公式的直接应用，要抓住恰好到达最高点的隐含条件是由重力来提供向心力，不难．
练习册系列答案
相关题目
如图所示，倾角为θ=45°的粗糙平直导轨与半径为R的光滑圆环轨道相切，切点为B，整个轨道处在竖直平面内．一质量为m的小滑块从导轨上离地面高为h=3R的D处无初速下滑进入圆环轨道．接着小滑块从圆环最高点C水平飞出，恰好击中导轨上与圆心O等高的P点，不计空气阻力．求：
如图所示，倾角为θ=45°的光滑平直斜轨与半径为R的光滑圆环轨道相切，切点为B，整个轨道处在竖直平面内．一质量为m的小球从斜轨上高为h的D处无初速度下滑进入圆环轨道．接着小球从圆环最高点C水平飞出，又落到轨道上，击中斜轨上的P点，且AP=
