题目内容
14.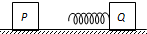 如图所示,质量均为m的小滑块P和Q都试作质点,与轻质弹簧相连的Q静止在光滑水平面上.P以某一初速度v0向Q运动并与弹簧发生碰撞,在整个过程中,弹簧具有的最大弹性势能等于多少?P最终的速度为多少?
如图所示,质量均为m的小滑块P和Q都试作质点,与轻质弹簧相连的Q静止在光滑水平面上.P以某一初速度v0向Q运动并与弹簧发生碰撞,在整个过程中,弹簧具有的最大弹性势能等于多少?P最终的速度为多少?
分析 当P、Q速度相等时,弹簧的弹性势能最大,根据动量守恒定律和机械能守恒定律求出弹簧的最大弹性势能.最终弹簧恢复原长,再由系统的动量守恒定律和机械能守恒定律求出P最终的速度.
解答 解:P、Q在相互作用过程中系统动量守恒,当两者具有相同速度时,弹簧压缩最多时,弹簧具有最大的弹性势能.取向右为正方向,由动量守恒定律得:
mv0=2mv
解得:v=0.5v0;
由机械能守恒定律得:
弹簧具有的最大弹性势能 Epm=$\frac{1}{2}$mv02-$\frac{1}{2}×2m{v}^{2}$=$\frac{1}{4}$mv02;
P和Q两者弹簧压缩后,当弹簧恢复原长,两者分离时,由动量守恒定律得:
mv0=mv1+mv2
由机械能守恒定律得:
$\frac{1}{2}$mv02=$\frac{1}{2}$mv12+$\frac{1}{2}$mv22
解得:P最终的速度 v1=0
答:弹簧具有的最大弹性势能是$\frac{1}{4}$mv02;P最终的速度是0.
点评 本题综合考查了动量守恒定律和能量守恒定律,关键知道当两者速度相同时,弹簧的弹性势能最大.要注意选取正方向.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.质点在合力F作用下以加速度a做匀变速直线运动,经过一段时间,质点的速度为vt,速度的改变量为△v,则( )
| A. | a与△v方向可能相反 | B. | a与F方向可能相反 | ||
| C. | a与vt方向一定相同 | D. | a与△v方向一定相同 |
5. 如图,一光滑的轻滑轮用细绳oo'悬挂于o点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一位于水平粗糙桌面上的物块b.外力F向右上方拉b,整个系统处于静止状态.若F方向不变,大小在一定范围内变化,物块b仍始终保持静止,则( )
如图,一光滑的轻滑轮用细绳oo'悬挂于o点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一位于水平粗糙桌面上的物块b.外力F向右上方拉b,整个系统处于静止状态.若F方向不变,大小在一定范围内变化,物块b仍始终保持静止,则( )
 如图,一光滑的轻滑轮用细绳oo'悬挂于o点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一位于水平粗糙桌面上的物块b.外力F向右上方拉b,整个系统处于静止状态.若F方向不变,大小在一定范围内变化,物块b仍始终保持静止,则( )
如图,一光滑的轻滑轮用细绳oo'悬挂于o点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一位于水平粗糙桌面上的物块b.外力F向右上方拉b,整个系统处于静止状态.若F方向不变,大小在一定范围内变化,物块b仍始终保持静止,则( )| A. | 绳oo'的张力也在一定范围内变化 | |
| B. | 物块b所受到的支持力也在一定范围内变化 | |
| C. | 连接a和b的绳的张力也在一定范围内变化 | |
| D. | 物块b与桌面间的摩擦力保持不变 |
2.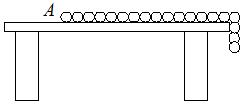 如图所示,有一根长为L,质量为M的均匀链条静止在光滑水平桌面上,其长度的$\frac{1}{5}$悬于桌边外,如果在链条的A端施加一个拉力使悬着的部分以0.1g(g为重力加速度)的加速度拉回桌面.设拉动过程中链条与桌边始终保持接触,则拉力最少需做功( )
如图所示,有一根长为L,质量为M的均匀链条静止在光滑水平桌面上,其长度的$\frac{1}{5}$悬于桌边外,如果在链条的A端施加一个拉力使悬着的部分以0.1g(g为重力加速度)的加速度拉回桌面.设拉动过程中链条与桌边始终保持接触,则拉力最少需做功( )
 如图所示,有一根长为L,质量为M的均匀链条静止在光滑水平桌面上,其长度的$\frac{1}{5}$悬于桌边外,如果在链条的A端施加一个拉力使悬着的部分以0.1g(g为重力加速度)的加速度拉回桌面.设拉动过程中链条与桌边始终保持接触,则拉力最少需做功( )
如图所示,有一根长为L,质量为M的均匀链条静止在光滑水平桌面上,其长度的$\frac{1}{5}$悬于桌边外,如果在链条的A端施加一个拉力使悬着的部分以0.1g(g为重力加速度)的加速度拉回桌面.设拉动过程中链条与桌边始终保持接触,则拉力最少需做功( )| A. | $\frac{MLg}{50}$ | B. | $\frac{MLg}{10}$ | C. | $\frac{MLg}{250}$ | D. | $\frac{MLg}{25}$ |
6.两个质量分别为m1和m2的物体,其间距离为r时,由万有引力定律可知,它们之间相互作用力的大小为F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$,式中G为引力常量.若用国际单位制的基本单位表示,G的单位应为( )
| A. | N•m2•kg-2 | B. | m3•s-2•kg-1 | C. | N•m2•kg-1 | D. | m3•s-2•kg-2 |
