题目内容
长为l的不计形变的轻绳，一端固定在O点，另一端系一质量为m小球，在O下方
处，将小球水平向右抛出，忽略空气阻力的影响，经过一段时间绳拉直（绳刚拉直时与竖直线夹角60°）；最后又摆动经过最低点．求：（1）球水平抛出的速度；
（2）球摆到最低点时，绳所受拉力．
【答案】分析：（1）平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动，根据高度求出时间，再根据水平位移和时间求出平抛运动的初速度．
（2）当绳子拉直后，沿绳子方向上的速度变为零，只剩下垂直于绳子方向上的分速度，根据机械能守恒定律求出小球摆动最低点的速度，再根据牛顿第二定律求出绳子的拉力．
解答：解：（1）小球平抛运动过程，则有
lsin60°=vt．
lcos60°-
=
gt2，
联立两式解得：v=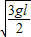
，t=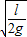
（2）绳子拉直时，小球在竖直方向上的分速度vy=gt=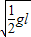
．
令此时球的速度与水平方向的夹角为θ
则tanθ=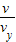
，得θ=30°
绳子拉直后，沿绳子方向上的速度变为零，只剩下垂直于绳子方向上的分速度，根据分解得：
v1=vysin60°-vsin30°=0
此后小球从静止开始做圆周运动．
根据机械能守恒定律得：
mv2=mgl（1-cos60°）
最低点：根据牛顿第二定律得：
F-mg=m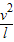
联立解得F=2mg．
答：（1）小球水平抛出时的初速度为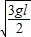
．
（2）小球摆到最低点时，绳所受的拉力为2mg．
点评：本题综合考查了平抛运动和圆周运动，关键掌握平抛运动在水平方向和竖直方向上的运动规律，以及能够熟练运用牛顿第二定律和机械能守恒定律．
（2）当绳子拉直后，沿绳子方向上的速度变为零，只剩下垂直于绳子方向上的分速度，根据机械能守恒定律求出小球摆动最低点的速度，再根据牛顿第二定律求出绳子的拉力．
解答：解：（1）小球平抛运动过程，则有
lsin60°=vt．
lcos60°-
=gt2，联立两式解得：v=
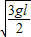，t=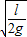（2）绳子拉直时，小球在竖直方向上的分速度vy=gt=
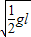．令此时球的速度与水平方向的夹角为θ
则tanθ=
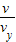，得θ=30°绳子拉直后，沿绳子方向上的速度变为零，只剩下垂直于绳子方向上的分速度，根据分解得：
v1=vysin60°-vsin30°=0
此后小球从静止开始做圆周运动．
根据机械能守恒定律得：
mv2=mgl（1-cos60°）最低点：根据牛顿第二定律得：
F-mg=m
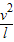
联立解得F=2mg．
答：（1）小球水平抛出时的初速度为
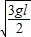．（2）小球摆到最低点时，绳所受的拉力为2mg．
点评：本题综合考查了平抛运动和圆周运动，关键掌握平抛运动在水平方向和竖直方向上的运动规律，以及能够熟练运用牛顿第二定律和机械能守恒定律．
练习册系列答案
相关题目
长为l的不计形变的轻绳，一端固定在O点，另一端系一质量为m小球，在O下方
如图所示，质量为M且足够长的木板在光滑的水平面上，其右端有一质量为m、可视为质点的滑块，滑块与木板间的动摩擦因数为μ．劲度系数为k的水平轻弹簧的右端O固定不动，其自由端A与滑块之间的距离为L．现给木板以水平向右的瞬时速度v0，滑块将由静止开始向右运动，与弹簧接触后经过时间t，滑块向右运动的速度达到最大，设滑块的速度始终小于木板的速度，弹簧的形变是在弹性限度内，重力加速度大小为g，不计空气阻力．求：
时（其中μ为工件与皮带之间的动摩擦因素），才有相对静止的过程，否则没有。
= 
（2）
。
。）
= m1
+ m2
+ m3
+ … + mn
只能是系统外力的矢量和，等式右边也是矢量相加。
x 。
Mg ，其中l＜L ，则x＜(L-l)的右段没有张力，x＞(L-l)的左端才有张力。
Mg时（μ为棒与平面的摩擦因素，l为小于L的某一值，M为棒的总质量），当x＜(L-l)，N≡0 ；当x＞(L-l)，N = 
〔x -〈L-l〉〕。
。
= m2a
g
。
= m1
+ m2
+ m3
+ … + mn
，猫和棒的系统外力只有两者的重力，竖直向下，而猫的加速度a1 = 0 ，所以：
g 。
。
求a1 。
。
at2 ②
a1xt2 ③
+ 
* = m 
（注：
*为惯性力），此题极简单。过程如下——
a相 t2 （3）