题目内容
18．
如图所示为回旋加速器的示意图．它由两个铝制D型金属扁盒组成，两个D形盒正中间开有一条狭缝；两个D型盒处在匀强磁场中并接在高频交变电源上．在D1盒中心A处有离子源，它产生并发出的正离子，经狭缝电压加速后，进入D2盒中．在磁场力的作用下运动半个圆周后，垂直通过狭缝，再经狭缝电压加速；为保证粒子每次经过狭缝都被加速，设法使交变电压的周期与粒子在狭缝及磁场中运动的周期一致．如此周而复始，速度越来越大，运动半径也越来越大，最后到达D型盒的边缘，以最大速度被导出．已知正离子是α粒子，其电荷量为q，质量为m，加速时电极间电压大小恒为U，磁场的磁感应强度为B，D型盒的半径为R，设狭缝很窄，粒子通过狭缝的时间可以忽略不计．设正离子从离子源发出时的初速度为零．（不计粒子重力）求：（1）α粒子在第n次加速后获得速率．
（2）α粒子在第n次加速后与第n+1次加速后位置之间的距离△x．
（3）若使用此回旋加速器加速氘核，要想使氘核获得与α粒子相同的动能，请你通过分析，提出一个简单可行的办法．
分析 （1）根据nqU=$\frac{1}{2}m{v}_{n}^{2}$，即可求解加速后获得速率．
（2）回旋加速器是利用电场加速和磁场偏转来加速粒子，根据动能定理求出n次加速后的速度，求出轨道半径，抓住规律，求出△x．
（3）回旋加速器加速粒子时，粒子在磁场中运动的周期和交流电变化的周期相同．已知氘核与α粒子的质量比和电荷比，根据最大动能相等，得出磁感应强度的关系，以及根据周期公式，得出交流电的周期变化．
解答 解：（1）α粒子在电场中被加速，根据动能定理，设此时的速度为vn，
则有：nqU=$\frac{1}{2}m{v}_{n}^{2}$，
解得：vn=$\sqrt{\frac{2nqU}{m}}$
（2）α粒子经电场第1次加速后，以速度v1进入D2盒，设轨道半径为r1
则 r1=$\frac{m{v}^{2}}{qB}$=$\frac{1}{B}\sqrt{\frac{2mU}{q}}$
α粒子经第2次电场加速后，以速度v2进入D1盒，设轨道半径为r2
则 r2=$\frac{m{v}^{2}}{qB}$=$\frac{1}{B}\sqrt{\frac{2×2mU}{q}}$
α粒子已经过n次电场加速，以速度vn进入D2盒，由动能定理：
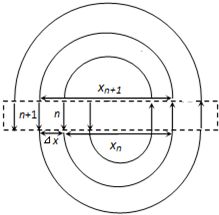
nUq=$\frac{1}{2}$m${v}_{n}^{2}$
轨道半径 rn=$\frac{m{v}_{n}}{qB}$=$\frac{1}{B}\sqrt{\frac{2nmU}{q}}$
α粒子已经过n+1次电场加速，以速度vn+1进入D1盒，由动能定理：
（n+1）Uq=$\frac{1}{2}$m${v}_{n+1}^{2}$
轨道半径：rn+1=$\frac{m{v}_{n+1}}{qB}$=$\frac{1}{B}\sqrt{\frac{（n+1）•2mU}{q}}$
则△x=2（rn+1-rn）（如图所示）
解得，△x=2（$\frac{1}{B}\sqrt{\frac{（n+1）•2mU}{q}}$-$\frac{1}{B}\sqrt{\frac{2nmU}{q}}$）=$\frac{2}{B}$$\sqrt{\frac{2Um}{q}}$（$\sqrt{n+1}$-$\sqrt{n}$）
（3）加速器加速带电粒子的能量为Ek=$\frac{1}{2}$mv2=$\frac{{q}^{2}{B}^{2}{R}^{2}}{2m}$，
由α粒子换成氘核，有$\frac{{q}^{2}{B}^{2}{R}^{2}}{2m}$=$\frac{（\frac{q}{2}）^{2}{B}_{1}^{2}{R}^{2}}{2（\frac{m}{2}）}$，则B1=$\sqrt{2}$B，即磁感应强度需增大为原来的$\sqrt{2}$ 倍；
高频交流电源的周期T=$\frac{2πm}{qB}$，由α粒子换为氘核时，交流电源的周期应为原来的$\frac{\sqrt{2}}{2}$倍．
答：（1）α粒子在第n次加速后获得速率$\sqrt{\frac{2nqU}{m}}$．
（2）α粒子在第n次加速后与第n+1次加速后位置之间的距离$\frac{2}{B}$$\sqrt{\frac{2Um}{q}}$（$\sqrt{n+1}$-$\sqrt{n}$）．
（3）若使用此回旋加速器加速氘核，要想使氘核获得与α粒子相同的动能，则磁感应强度需增大为原来的$\sqrt{2}$ 倍，或者交流电源的周期应为原来的$\frac{\sqrt{2}}{2}$倍．
点评 解决本题的关键知道回旋加速器利用磁场偏转和电场加速实现加速粒子，粒子在磁场中运动的周期和交流电的周期相等．
在研究平抛物体运动的实验中，用一张印有小方格的纸记录轨迹，小方格的边长l=1dm，若小球在平抛运动途中的几个位置如图中的a、b、c、d所示，则小球平抛的初速度的计算式为v0=2$\sqrt{gL}$（用l、g表示），其值是2（取g=10m/s2）
如图，斜面与水平面之间的夹角为45°，在斜面底端A点正上方高度为10m处的O点，以5m/s的速度水平抛出一个小球，飞行一段时间后撞在斜面上，这段飞行所用的时间为（g=10m/s2）（ ）| A． | 2 s | B． | $\sqrt{2}$ s | C． | 1 s | D． | 0.5 s |
| A． | 医学上利用γ射线治疗肿瘤主要是利用了γ射线的穿透能力强的特点 | |
| B． | 若用频率更高的单色光照射时，同级牛顿环半径将会变大 | |
| C． | 机械波在传播波源的振动的形式的同时传递了能量 | |
| D． | 麦克耳孙-莫雷实验表明：不论光源与观察者做怎样的相对运动，光速都是一样的 |
| A． | 107J | B． | 108J | C． | 109J | D． | 1010J |
如图所示，条形磁场组方向水平向里，磁场边界与地面平行，磁场区域宽度为L=0.1m，磁场间距为2L，一正方形金属线框质量为m=0.1kg，边长也为L，总电阻为R=0.02Ω．现将金属线框置于磁场区域1上方某一高度h处自由释放，线框在经过磁场区域时bc边始终与磁场边界平行．当h=2L时，bc边进入磁场时金属线框刚好能做匀速运动．不计空气阻力，重力加速度g取10m/s2．| A． | 电场力对液滴做的功为$\frac{1}{2}$vm02 | |
| B． | 液滴克服电场力做的功为$\frac{1}{2}$vm02+mgh | |
| C． | 液滴的机械能减少mgh | |
| D． | 液滴的电势能增加mgh |
| A． | 如果线速度大小不变，角速度变为原来的2倍 | |
| B． | 如果角速度不变，周期变为原来的2倍 | |
| C． | 如果周期不变，向心加速度大小变为原来的2倍 | |
| D． | 如果角速度不变，线速度大小变为原来的2倍 |
