题目内容
2．
如图，在斜面顶端的A点以速度v平抛一小球，经t1时间落到斜面上B点处，若在A点将此小球以速度$\frac{v}{3}$水平抛出，经t2时间落到斜面上的C点处，以下判断正确的是（ ）| A． | AB：AC=3：1 | B． | AB：AC=9：1 | C． | t1：t2=9：1 | D． | t1：t2=$\sqrt{3}$：1 |
分析 根据竖直位移和水平位移的关系得出运动时间的表达式，结合初速度之比求出运动时间之比．根据初速度和时间，结合平行四边形定则求出抛出点和落地点间的距离表达式，从而得出AB和AC的距离之比．
解答 解：根据tanθ=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}=\frac{gt}{2{v}_{0}}$得，小球平抛运动的时间t=$\frac{2{v}_{0}tanθ}{g}$，
因为抛出的初速度之比为3：1，则运动的时间之比t1：t2=3：1，故C错误，D错误．
落地点与抛出点间的距离s=$\frac{{v}_{0}t}{cosθ}=\frac{2{{v}_{0}}^{2}tanθ}{gcosθ}$，由于初速度之比为3：1，则AB：AC=9：1，故B正确，A错误．
故选：B．
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律，结合运动学公式灵活求解，难度不大．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
11．
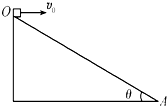如图所示，足够长斜面OA的倾角为θ，固定在水平地面上，现从顶点O以速度v0平抛一小球，不计空气阻力，重力加速度为g，求小球在飞行过程中与斜面之间的最远距离（ ）•
如图所示，足够长斜面OA的倾角为θ，固定在水平地面上，现从顶点O以速度v0平抛一小球，不计空气阻力，重力加速度为g，求小球在飞行过程中与斜面之间的最远距离（ ）•| A． | $\frac{{v}_{0}sinθ}{2g}$ | B． | $\frac{{{v}_{0}}^{2}}{2g}$ | ||
| C． | $\frac{{{v}_{0}}^{2}sinθ}{2gcosθ}$ | D． | $\frac{{{v}_{0}}^{2}si{n}^{2}θ}{2gcosθ}$ |
10．列关于物理学思想和方法的叙述错误的是（ ）
| A． | 在推导匀变速直线运动位移公式时，把整个运动过程划分成很多小段，每一小段近似看作匀速直线运动，再把各小段位移相加，这里运用了微元法 | |
| B． | 探究加速度与力和质量关系的实验运用了控制变量法 | |
| C． | 当物体的运动时间△t趋近于0时，△t时间内的平均速度可看成瞬时速度运用了等效替代法 | |
| D． | 奥斯特发现电生磁到法拉第发现磁生电的过程中运用了逆向思维法 |
某同学先用欧姆表的“×10”档粗测一电阻阻值，欧姆表示数如图所示，给出下列仪器供选用：
14．
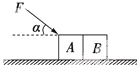如图所示，物体A、B与地面间动摩擦因数相同，质量也相同，在力F的作用下一起沿水平地面运动了距离s，以下说法中正确的是（ ）
如图所示，物体A、B与地面间动摩擦因数相同，质量也相同，在力F的作用下一起沿水平地面运动了距离s，以下说法中正确的是（ ）| A． | 摩擦力对A、B所做的功相同 | B． | 合外力对A、B所做的功相同 | ||
| C． | F对A所做的功与A对B做的功相同 | D． | A对B的作用力大于B对A的作用力 |
11．2013年6月11日“神舟十号”顺利升空，标志着我国火箭载人太空飞行有了历史性的跨越，高空实验火箭起飞前，仪器舱内气体的压强p0=1atm，温度t0=27℃，在火箭竖直向上飞行的过程中，加速度的大小等于重力加速度g，仪器舱内水银气压计是示数为p=0.6p0，已知仪器舱是密封的，那么，这段过程中舱内温度是（ ）
| A． | 16.2℃ | B． | 32.4℃ | C． | 360K | D． | 180K |
12．宇宙中有一半径为R的星球，宇航员站在该星球上离星球表面h高处以速度v平行星球表面抛出一质量为m的小球，测得小球的水平位移为x，这一平抛运动的空间范围很小，可不计重力加速度的变化．下列判断正确的是（ ）
| A． | 在该星球表面上以v0=$\frac{v}{x}$$\sqrt{2Rh}$的初速度水平抛出一物体，物体将不再落回星球表面 | |
| B． | 在该星球表面上以v0=$\frac{v}{x}$$\sqrt{2Rh}$的初速度水平抛出一物体，物体将落回星球表面 | |
| C． | 绕距离该星球表面高为R运行的卫星的向心加速度为a=$\frac{2h{v}^{2}}{{x}^{2}}$ | |
| D． | 绕该星球表面附近运行的卫星的周期为T=$\frac{2πr}{v}$ |