Question

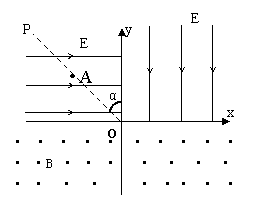
在xoy平面内，直线OP与y轴的夹角α＝45⁰。第一、第二象限内存在大小相等，方向分别为竖直向下和水平向右的匀强电场E；在x轴下方有垂直于纸面向外的匀强磁场B，如图所示。现有一带正电的粒子从直线OP上某点A（－L，L）处静止释放。设粒子的比荷=，粒子重力不计，其中E、B、m、q均未知。求：

（1）粒子进入磁场时与x轴交点的横坐标

（2）粒子进入磁场时速度方向与x轴正方向的夹角

（3）如果在直线OP上各点释放许多个上述带电粒子（粒子间的相互作用力不计），试证明各带电粒子  进入磁场后做圆周运动的圆心点的集合为一抛物线（提示：写出圆心点坐标x、y的函数关系）

Answer 1

解析：⑴设粒子进入第一象限的初速度为v₁,由动能定理得：

                     ① 

粒子在第一象限作类平抛运动，                                     ②

                                   ③

                                      ④

                       得：x=2L                                        ⑤

⑵类平抛运动过程的末速度设为v,竖直分速度为Vy,

V_y=at,               ⑥

              

 = V₁         ⑦

              ⑧

 φ＝45⁰                         ⑨

∴v与x轴正方向的夹角为45⁰。

⑶L取任意值时均有：

X=2L , α=45⁰

          ⑩

粒子在磁场中做匀速圆周运动时，                     ⑾

将代入上式得

                             ⑿

所以圆心的坐标为：

                ⒀

代入并消去L，得

                                  ⒁

此方程为一抛物线方程

评分标准：（1）问7分，其中①⑤各式2分,②③④每式各1分；（2）问7分，其中⑥式1分，⑦～⑨每式2分；（3）问8分。⑩⑾各1分，⑿～⒁式各2分。