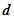题目内容
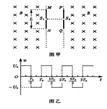
如图甲所示,相隔一定距离的竖直边界两侧为相同的匀 强磁场区,磁场方向垂直纸面向里,在边界上固定两长为L的平行金属极板MN和PQ,两极板中心各有一小孔![]() 、
、![]() ,两极板间电压的变化规律如图乙所示,正反向电压的大小均为
,两极板间电压的变化规律如图乙所示,正反向电压的大小均为![]() ,周期为
,周期为![]() 。在
。在![]() 时刻将一个质量为
时刻将一个质量为![]() 、电量为
、电量为![]() (
(![]() )的粒子由
)的粒子由![]() 静止释放,粒子在电场力的作用下向右运动,在
静止释放,粒子在电场力的作用下向右运动,在![]() 时刻通过
时刻通过![]() 垂直于边界进入右侧磁场区。(不计粒子重力,不考虑极板外的电场)
垂直于边界进入右侧磁场区。(不计粒子重力,不考虑极板外的电场)
(1)求粒子到达![]() 时德 速度大小
时德 速度大小![]() 和极板距离
和极板距离![]() 。
。
(2)为使粒子不与极板相撞,求磁感应强度的大小应满足的条件。
(3)若已保证了粒子未与极板相撞,为使粒子在![]() 时刻再次到达
时刻再次到达![]() ,且速度恰好为零,求该过程中粒子在磁场内运动的时间和磁感强度的大小
,且速度恰好为零,求该过程中粒子在磁场内运动的时间和磁感强度的大小

(1)粒子由![]() 至
至![]() 的过程中,根据动能定理得
的过程中,根据动能定理得

![]()
由![]() 式得
式得

![]()
设粒子的加速度大小为![]() ,由牛顿第二定律得
,由牛顿第二定律得

![]()
由运动学公式得

![]()
联立![]()
![]() 式得
式得

![]()
(2)设磁感应强度大小为B,粒子在磁场中做匀速圆周运动的半径为R,由牛顿第二定律得

![]()
要使粒子在磁场中运动时不与极板相撞,须满足

![]()
联立![]()
![]()
![]() 式得
式得

![]()
(3)设粒子在两边界之间无场区向左匀速运动的过程用时为![]() ,有
,有
![]()
![]()
联立![]()
![]()
![]() 式得
式得

![]()
若粒子再次达到![]() 时速度恰好为零,粒子回到极板间应做匀减速运动,设匀减速运动的时间为
时速度恰好为零,粒子回到极板间应做匀减速运动,设匀减速运动的时间为![]() ,根据运动学公式得
,根据运动学公式得

![]()
联立![]()
![]()
![]() 式得
式得

![]()
设粒子在磁场中运动的时间为![]()

![]()
联立![]()
![]()
![]() 式得
式得

![]()
设粒子在匀强磁场中做匀速圆周运动的周期为T,由![]() 式结合运动学公式得
式结合运动学公式得

![]()
由题意得
![]()
![]()
联立![]()
![]()
![]() 式得
式得

![]()

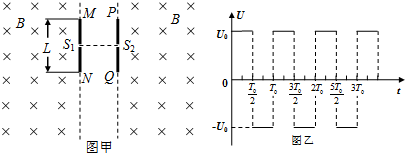
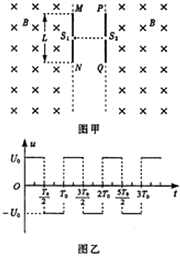 如图甲所示,相隔一定距离的竖直边界两侧为相同的匀强磁场区,磁场方向垂直纸面向里,在边界上固定两长为L的平行金属极板MN和PQ,两极板中心各有一小孔S1、S2,两极板间电压的变化规律如图乙所示,正反向电压的大小均为U0,周期为T0.在t=0时刻将一个质量为m、电量为-q(q>0)的粒子由S1静止释放,粒子在电场力的作用下向右运动,在
如图甲所示,相隔一定距离的竖直边界两侧为相同的匀强磁场区,磁场方向垂直纸面向里,在边界上固定两长为L的平行金属极板MN和PQ,两极板中心各有一小孔S1、S2,两极板间电压的变化规律如图乙所示,正反向电压的大小均为U0,周期为T0.在t=0时刻将一个质量为m、电量为-q(q>0)的粒子由S1静止释放,粒子在电场力的作用下向右运动,在 、
、 ,两极板间电压的变化规律如图乙所示,正反向电压的大小均为
,两极板间电压的变化规律如图乙所示,正反向电压的大小均为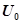 ,周期为
,周期为 。在
。在 时刻将一个质量为
时刻将一个质量为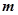 、电量为
、电量为 (
( )的粒子由
)的粒子由 时刻通过
时刻通过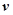 和极板距离
和极板距离
 、
、 ,两极板间电压的变化规律如图乙所示,正反向电压的大小均为
,两极板间电压的变化规律如图乙所示,正反向电压的大小均为 ,周期为
,周期为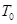 。在
。在 时刻将一个质量为
时刻将一个质量为 、电量为
、电量为 (
( )的粒子由
)的粒子由 时刻通过
时刻通过
 和极板距离
和极板距离
 时刻再次到达
时刻再次到达 、
、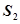 ,两极板间电压的变化规律如图乙所示,正反向电压的大小均为
,两极板间电压的变化规律如图乙所示,正反向电压的大小均为 ,周期为
,周期为 。在
。在 时刻将一个质量为
时刻将一个质量为 、电量为
、电量为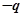 (
(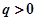 )的粒子由
)的粒子由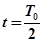 时刻通过
时刻通过 和极板距离
和极板距离