题目内容
5.如图甲所示,在倾角θ=300的光滑绝缘斜面上,水平虚线ab、cd、ef、gh为等间距分布,其间距l=0.5m,在ab与cd间、ef与gh间均存在有垂直斜面向下的匀强磁场,磁感应强度B随时间t的变化图象如图乙所示.现有一长方形金属线框PQMN用绝缘绳系于斜面上,PQ与虚线平行且处在ab、cd的中间. 已知PQ=MN=0.4m,PN=QM=1.0m,金属线框的电阻R=0.04Ω.当t=$\frac{1}{16}$s时刻绳子拉力恰好为零.若此时将绳子剪断,线框从静止开始向下运动,当边MN刚进入ef和gh之间的磁场区域时,线框恰好做匀速运动.(空气阻力不计,g取10m/s2)求: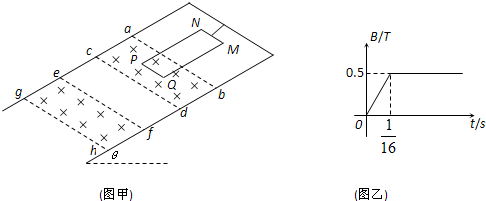
(1)线框的质量m;
(2)当边MN刚进入ef时的速度大小v2?
(3)PQ边到达cd开始计时到当边MN刚进入ef过程中是什么运动性质(匀加速还是变加速)?PQ边到达cd时速度的大小v1;
(4)线框从开始运动到通过两个磁场区域的过程中产生的电热Q.
分析 (1)在0-$\frac{1}{16}$s内,根据法拉第电磁感应定律、欧姆定律求出感应电流.根据当t=$\frac{1}{16}$s时刻绳子拉力恰好为零,线框受力平衡列式,可求得线框的质量m;
(2)当边MN刚进入ef和gh之间的磁场区域时,线框恰好做匀速运动,受力平衡,由安培力公式和平衡条件结合求解v2;
(3)从PQ到达cd至MN到达ef,穿过线框的磁通量不变,不产生感应电流,不受安培力,线框以加速度 a=gsin30°作匀加速直线运动.由运动学公式求解PQ边到达cd时速度的大小v1.
(4)线框从开始运动到通过两个磁场区域的过程,运用能量守恒列式求解热量Q.
解答 解:(1)在0-$\frac{1}{16}$s内,$\frac{△B}{△t}$=8T/s
s=$\frac{1}{2}l\overline{PQ}$=$\frac{1}{2}×0.5×0.4$=0.1m2;
根据法拉第电磁感应定律得:
E=$\frac{△Φ}{△t}$=$\frac{△B}{△t}$s=0.8V
i=$\frac{E}{R}$=20A
线框静止时:mgsin30°=BIL
解得:m=0.8kg
(2)MN到达ef时匀速运动,则有:mgsin30°=$\frac{{B}^{2}{l}^{2}{v}_{2}}{R}$
解得:v2=4m/s
(3)从PQ到达cd至MN到达ef,穿过线框的磁通量不变,不产生感应电流,不受安培力,所以线框以加速度 a=gsin30°作匀加速直线运动.
由${v}_{2}^{2}-{v}_{1}^{2}$=2a•3l,其中 l=0.5m
解得:v1=1m/s
(3)由能量守恒得:
mg$•\frac{9l}{2}$sin30°=$\frac{1}{2}m{v}_{2}^{2}$+Q
解得:Q=2.6J
答:(1)线框的质量m是0.8kg;
(2)当边MN刚进入ef时的速度大小v2是4m/s.
(3)PQ边到达cd开始计时到当边MN刚进入ef过程中是匀加速运动,PQ边到达cd时速度的大小v1是1m/s.
(4)线框从开始运动到通过两个磁场区域的过程中产生的电热Q是2.6J.
点评 解决这类问题的关键是正确分析电路中的电流以及安培力的变化情况,判断线框的受力情况,结合电磁感应和力学规律解答.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案 如图所示,一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )
如图所示,一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )| A. | 球A的线速度一定大于球B的线速度 | |
| B. | 球A的角速度一定大于球B的角速度 | |
| C. | 球A的运动周期一定小于球B的运动周期 | |
| D. | 球A对筒壁的压力等于球B对筒壁的压力 |
| A. | 卢瑟福通过a粒子散射实验建立了原子核式结构模型 | |
| B. | 根据玻尔理论可知,当氢原子从n=4的状态跃迁到n=2的状态时,发射出光子 | |
| C. | β衰变中产生的β射线实际上是原子的核外电子挣脱原子核的束缚而形成的 | |
| D. | ${\;}_{86}^{222}$Rn的半衰期为3.8天,若有20g${\;}_{86}^{222}$Rn,经过7.6天后还剩下5g${\;}_{86}^{222}$Rn | |
| E. | 一束光照射到某种金属上不能发生光电效应,可能是因为这束光的光强太小 |
| A. | 质量 时间 | B. | 速度 时间 | C. | 秒 千克 | D. | 牛顿 焦耳 |
 如图所示,两块水平放置、相距为d的长金属板接在电压可调的电源上.两板之间的右侧区域存在方向垂直纸面向里的匀强磁场.将喷墨打印机的喷口靠近上板下表面,从喷口连续不断喷出质量均为m、水平速度均为v0、带相等电荷量的墨滴.调节电源电压至U,墨滴在电场区域恰能沿水平向右做匀速直线运动;进入电场、磁场共存区域后,最终垂直打在下板的M点.
如图所示,两块水平放置、相距为d的长金属板接在电压可调的电源上.两板之间的右侧区域存在方向垂直纸面向里的匀强磁场.将喷墨打印机的喷口靠近上板下表面,从喷口连续不断喷出质量均为m、水平速度均为v0、带相等电荷量的墨滴.调节电源电压至U,墨滴在电场区域恰能沿水平向右做匀速直线运动;进入电场、磁场共存区域后,最终垂直打在下板的M点.
 如图所示,固定在水平面上的金属框架cdef,处在竖直向下的匀强磁场中,金属棒ab搁在框架上,可无摩擦滑动.此时,adeb构成一个边长为l的正方形.棒的电阻为r,其余部分电阻不计.开始时磁感应强度为B0.
如图所示,固定在水平面上的金属框架cdef,处在竖直向下的匀强磁场中,金属棒ab搁在框架上,可无摩擦滑动.此时,adeb构成一个边长为l的正方形.棒的电阻为r,其余部分电阻不计.开始时磁感应强度为B0. 一简谐横波沿x轴正方向传播,若在x=1m处质点的振动图象如图所示,则该波在t=0.3s时刻的波形曲线为( )
一简谐横波沿x轴正方向传播,若在x=1m处质点的振动图象如图所示,则该波在t=0.3s时刻的波形曲线为( )


