题目内容

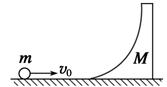
光滑水平面上放着一质量为M的槽，槽与水平面相切且光滑，如图所示，一质量为m的小球以速度v0向槽运动，若开始时槽固定不动，求小球上升的最大高度(槽足够高)．若槽不固定，则小球又上升多高？

 

【答案】

 

【解析】

试题分析：槽固定时，设球上升的最大高度为h1，由机械能守恒得mgh1＝mv，解得h1＝；

槽不固定时，设球上升的最大高度为h2，此时两者有共同速度v，由动量守恒定律得：mv0＝(m＋M)v.由机械能守恒得：mv＝ (m＋M)v2＋mgh2，解得槽不固定时小球上升的高度h2＝.

考点：动量守恒 机械能守恒

点评：本题的关键是找到小滑块上升到最高点的条件是滑块竖直方向的速度为零，而水平方向动量守恒，这是一道考查动量守恒和机械能守恒的好题．

 

练习册系列答案
相关题目
如图所示，在光滑的水平面上停放着一辆平板车，在车上的左端放有一木块B．车左边紧邻一个固定在竖直面内、半径为R的
14
圆弧形光滑轨道，已知轨道底端的切线水平，且高度与车表面相平．现有另一木块A（木块A、B均可视为质点）从圆弧轨道的顶端由静止释放，然后滑行到车上与B发生碰撞．两木块碰撞后立即粘在一起在平板车上滑行，并与固定在平板车上的水平轻质弹簧作用后被弹回，最后两木块刚好回到车的最左端与车保持相对静止．已知木块A的质量为m，木块B的质量为2m，车的质量为3m，重力加速度为g，设木块A、B碰撞的时间极短可以忽略．求：
（1）木块A、B碰撞后的瞬间两木块共同运动速度的大小．
（2）木块A、B在车上滑行的整个过程中，木块和车组成的系统损失的机械能．
（3）弹簧在压缩过程中所具有的最大弹性势能．
如图所示，在光滑水平面上放着长为L，质理量为M的长木板，在长木板左端放一质量为m的物块（可视为质点），开始物体和长木板均处于静止状态，物块和长木板间的接触是粗糙的。今对物块m施一水平向右的恒力F，物块与木板分离时木板的速度为v。下列判断正确的是      
A．若只增大物块质量m，则相对滑动过程木板的加速度不变，但分离时速度v变大
B．若只增大物块质量m，则相对滑动过程木板的加速度增大，但分离时速度v变小    
C．若只增大恒力F，则相对滑动过程木板的加速度增大，分离时v也变大  
D．若只增大恒力F，则相对滑动过程木板的加速度不变，但分离时v变小

（15分）光滑水平面上放着质量为mA＝1Ikg 的物块A与质量脚，mB＝2kg的物块B, A 与B均可视为质点，A靠在竖直墙壁上，A、B间夹一个被压缩的轻弹簧（弹簧与A、B均不拴接），用手挡住B不动，此时弹簧弹性势能EP＝49J。在A、B间系一轻质细绳，细绳长度大于弹簧的自然长度，如图一所示。放手后B向右运动，绳在短暂时间内被拉断，之后B冲上与水平面相切的竖直半圆光滑轨道，其半径R＝0.5.m , B恰能到达最高点C。g＝10m/s2。求

（1）绳拉断后瞬间B的速度vB的大小；
（2）绳拉断过程绳对B的冲量I；

（3）绳拉断过程绳对A所做的功W。

第二部分  牛顿运动定律

第一讲 牛顿三定律

一、牛顿第一定律

1、定律。惯性的量度

2、观念意义，突破“初态困惑”

二、牛顿第二定律

1、定律

2、理解要点

a、矢量性

b、独立作用性：ΣF → a ，ΣFx → ax …

c、瞬时性。合力可突变，故加速度可突变（与之对比：速度和位移不可突变）；牛顿第二定律展示了加速度的决定式（加速度的定义式仅仅展示了加速度的“测量手段”）。

3、适用条件

a、宏观、低速

b、惯性系

对于非惯性系的定律修正——引入惯性力、参与受力分析

三、牛顿第三定律

1、定律

2、理解要点

a、同性质（但不同物体）

b、等时效（同增同减）

c、无条件（与运动状态、空间选择无关）

第二讲 牛顿定律的应用

一、牛顿第一、第二定律的应用

单独应用牛顿第一定律的物理问题比较少，一般是需要用其解决物理问题中的某一个环节。

应用要点：合力为零时，物体靠惯性维持原有运动状态；只有物体有加速度时才需要合力。有质量的物体才有惯性。a可以突变而v、s不可突变。

1、如图1所示，在马达的驱动下，皮带运输机上方的皮带以恒定的速度向右运动。现将一工件（大小不计）在皮带左端A点轻轻放下，则在此后的过程中（      ）

A、一段时间内，工件将在滑动摩擦力作用下，对地做加速运动

B、当工件的速度等于v时，它与皮带之间的摩擦力变为静摩擦力

C、当工件相对皮带静止时，它位于皮带上A点右侧的某一点

D、工件在皮带上有可能不存在与皮带相对静止的状态

解说：B选项需要用到牛顿第一定律，A、C、D选项用到牛顿第二定律。

较难突破的是A选项，在为什么不会“立即跟上皮带”的问题上，建议使用反证法（t → 0 ，a → ∞ ，则ΣFx → ∞ ，必然会出现“供不应求”的局面）和比较法（为什么人跳上速度不大的物体可以不发生相对滑动？因为人是可以形变、重心可以调节的特殊“物体”）

此外，本题的D选项还要用到匀变速运动规律。用匀变速运动规律和牛顿第二定律不难得出

只有当L ＞ 时（其中μ为工件与皮带之间的动摩擦因素），才有相对静止的过程，否则没有。

答案：A、D

思考：令L = 10m ，v = 2 m/s ，μ= 0.2 ，g取10 m/s2 ，试求工件到达皮带右端的时间t（过程略，答案为5.5s）

进阶练习：在上面“思考”题中，将工件给予一水平向右的初速v0 ，其它条件不变，再求t（学生分以下三组进行）——

① v0 = 1m/s  (答：0.5 + 37/8 = 5.13s)

② v0 = 4m/s  (答：1.0 + 3.5 = 4.5s)

③ v0 = 1m/s  (答：1.55s)

2、质量均为m的两只钩码A和B，用轻弹簧和轻绳连接，然后挂在天花板上，如图2所示。试问：

① 如果在P处剪断细绳，在剪断瞬时，B的加速度是多少？

② 如果在Q处剪断弹簧，在剪断瞬时，B的加速度又是多少？

解说：第①问是常规处理。由于“弹簧不会立即发生形变”，故剪断瞬间弹簧弹力维持原值，所以此时B钩码的加速度为零（A的加速度则为2g）。

第②问需要我们反省这样一个问题：“弹簧不会立即发生形变”的原因是什么？是A、B两物的惯性，且速度v和位移s不能突变。但在Q点剪断弹簧时，弹簧却是没有惯性的（没有质量），遵从理想模型的条件，弹簧应在一瞬间恢复原长！即弹簧弹力突变为零。

答案：0 ；g 。

二、牛顿第二定律的应用

应用要点：受力较少时，直接应用牛顿第二定律的“矢量性”解题。受力比较多时，结合正交分解与“独立作用性”解题。

在难度方面，“瞬时性”问题相对较大。

1、滑块在固定、光滑、倾角为θ的斜面上下滑，试求其加速度。

解说：受力分析 → 根据“矢量性”定合力方向 → 牛顿第二定律应用

答案：gsinθ。

思考：如果斜面解除固定，上表仍光滑，倾角仍为θ，要求滑块与斜面相对静止，斜面应具备一个多大的水平加速度？（解题思路完全相同，研究对象仍为滑块。但在第二环节上应注意区别。答：gtgθ。）

进阶练习1：在一向右运动的车厢中，用细绳悬挂的小球呈现如图3所示的稳定状态，试求车厢的加速度。（和“思考”题同理，答：gtgθ。）

进阶练习2、如图4所示，小车在倾角为α的斜面上匀加速运动，车厢顶用细绳悬挂一小球，发现悬绳与竖直方向形成一个稳定的夹角β。试求小车的加速度。

解：继续贯彻“矢量性”的应用，但数学处理复杂了一些（正弦定理解三角形）。

分析小球受力后，根据“矢量性”我们可以做如图5所示的平行四边形，并找到相应的夹角。设张力T与斜面方向的夹角为θ，则

θ=（90°+ α）- β= 90°-（β-α）                 （1）

对灰色三角形用正弦定理，有

 =                                        （2）

解（1）（2）两式得：ΣF = 

最后运用牛顿第二定律即可求小球加速度（即小车加速度）

答： 。

2、如图6所示，光滑斜面倾角为θ，在水平地面上加速运动。斜面上用一条与斜面平行的细绳系一质量为m的小球，当斜面加速度为a时（a＜ctgθ），小球能够保持相对斜面静止。试求此时绳子的张力T 。

解说：当力的个数较多，不能直接用平行四边形寻求合力时，宜用正交分解处理受力，在对应牛顿第二定律的“独立作用性”列方程。

正交坐标的选择，视解题方便程度而定。

解法一：先介绍一般的思路。沿加速度a方向建x轴，与a垂直的方向上建y轴，如图7所示（N为斜面支持力）。于是可得两方程

ΣFx = ma ，即Tx － Nx = ma

ΣFy = 0 ， 即Ty + Ny = mg

代入方位角θ，以上两式成为

T cosθ－N sinθ = ma                       （1）

T sinθ + Ncosθ = mg                       （2）

这是一个关于T和N的方程组，解（1）（2）两式得：T = mgsinθ + ma cosθ

解法二：下面尝试一下能否独立地解张力T 。将正交分解的坐标选择为：x——斜面方向，y——和斜面垂直的方向。这时，在分解受力时，只分解重力G就行了，但值得注意，加速度a不在任何一个坐标轴上，是需要分解的。矢量分解后，如图8所示。

根据独立作用性原理，ΣFx = max

即：T － Gx = max

即：T － mg sinθ = m acosθ

显然，独立解T值是成功的。结果与解法一相同。

答案：mgsinθ + ma cosθ

思考：当a＞ctgθ时，张力T的结果会变化吗？（从支持力的结果N = mgcosθ－ma sinθ看小球脱离斜面的条件，求脱离斜面后，θ条件已没有意义。答：T = m 。）

学生活动：用正交分解法解本节第2题“进阶练习2”

进阶练习：如图9所示，自动扶梯与地面的夹角为30°，但扶梯的台阶是水平的。当扶梯以a = 4m/s2的加速度向上运动时，站在扶梯上质量为60kg的人相对扶梯静止。重力加速度g = 10 m/s2，试求扶梯对人的静摩擦力f 。

解：这是一个展示独立作用性原理的经典例题，建议学生选择两种坐标（一种是沿a方向和垂直a方向，另一种是水平和竖直方向），对比解题过程，进而充分领会用牛顿第二定律解题的灵活性。

答：208N 。

3、如图10所示，甲图系着小球的是两根轻绳，乙图系着小球的是一根轻弹簧和轻绳，方位角θ已知。现将它们的水平绳剪断，试求：在剪断瞬间，两种情形下小球的瞬时加速度。

解说：第一步，阐明绳子弹力和弹簧弹力的区别。

（学生活动）思考：用竖直的绳和弹簧悬吊小球，并用竖直向下的力拉住小球静止，然后同时释放，会有什么现象？原因是什么？

结论——绳子的弹力可以突变而弹簧的弹力不能突变（胡克定律）。

第二步，在本例中，突破“绳子的拉力如何瞬时调节”这一难点（从即将开始的运动来反推）。

知识点，牛顿第二定律的瞬时性。

答案：a甲 = gsinθ ；a乙 = gtgθ 。

应用：如图11所示，吊篮P挂在天花板上，与吊篮质量相等的物体Q被固定在吊篮中的轻弹簧托住，当悬挂吊篮的细绳被烧断瞬间，P、Q的加速度分别是多少？

解：略。

答：2g ；0 。

三、牛顿第二、第三定律的应用

要点：在动力学问题中，如果遇到几个研究对象时，就会面临如何处理对象之间的力和对象与外界之间的力问题，这时有必要引进“系统”、“内力”和“外力”等概念，并适时地运用牛顿第三定律。

在方法的选择方面，则有“隔离法”和“整体法”。前者是根本，后者有局限，也有难度，但常常使解题过程简化，使过程的物理意义更加明晰。

对N个对象，有N个隔离方程和一个（可能的）整体方程，这（N + 1）个方程中必有一个是通解方程，如何取舍，视解题方便程度而定。

补充：当多个对象不具有共同的加速度时，一般来讲，整体法不可用，但也有一种特殊的“整体方程”，可以不受这个局限（可以介绍推导过程）——

Σ= m1 + m2 + m3 + … + mn

其中Σ只能是系统外力的矢量和，等式右边也是矢量相加。

1、如图12所示，光滑水平面上放着一个长为L的均质直棒，现给棒一个沿棒方向的、大小为F的水平恒力作用，则棒中各部位的张力T随图中x的关系怎样？

解说：截取隔离对象，列整体方程和隔离方程（隔离右段较好）。

答案：N = x 。

思考：如果水平面粗糙，结论又如何？

解：分两种情况，（1）能拉动；（2）不能拉动。

第（1）情况的计算和原题基本相同，只是多了一个摩擦力的处理，结论的化简也麻烦一些。

第（2）情况可设棒的总质量为M ，和水平面的摩擦因素为μ，而F = μMg ，其中l＜L ，则x＜(L-l)的右段没有张力，x＞(L-l)的左端才有张力。

答：若棒仍能被拉动，结论不变。

若棒不能被拉动，且F = μMg时（μ为棒与平面的摩擦因素，l为小于L的某一值，M为棒的总质量），当x＜(L-l)，N≡0 ；当x＞(L-l)，N = 〔x -〈L-l〉〕。

应用：如图13所示，在倾角为θ的固定斜面上，叠放着两个长方体滑块，它们的质量分别为m1和m2 ，它们之间的摩擦因素、和斜面的摩擦因素分别为μ1和μ2 ，系统释放后能够一起加速下滑，则它们之间的摩擦力大小为：

A、μ1 m1gcosθ ；    B、μ2 m1gcosθ ；

C、μ1 m2gcosθ ；    D、μ1 m2gcosθ ；

解：略。

答：B 。（方向沿斜面向上。）

思考：（1）如果两滑块不是下滑，而是以初速度v0一起上冲，以上结论会变吗？（2）如果斜面光滑，两滑块之间有没有摩擦力？（3）如果将下面的滑块换成如图14所示的盒子，上面的滑块换成小球，它们以初速度v0一起上冲，球应对盒子的哪一侧内壁有压力？

解：略。

答：（1）不会；（2）没有；（3）若斜面光滑，对两内壁均无压力，若斜面粗糙，对斜面上方的内壁有压力。

2、如图15所示，三个物体质量分别为m1 、m2和m3 ，带滑轮的物体放在光滑水平面上，滑轮和所有接触面的摩擦均不计，绳子的质量也不计，为使三个物体无相对滑动，水平推力F应为多少？

解说：

此题对象虽然有三个，但难度不大。隔离m2 ，竖直方向有一个平衡方程；隔离m1 ，水平方向有一个动力学方程；整体有一个动力学方程。就足以解题了。

答案：F =  。

思考：若将质量为m3物体右边挖成凹形，让m2可以自由摆动（而不与m3相碰），如图16所示，其它条件不变。是否可以选择一个恰当的F′，使三者无相对运动？如果没有，说明理由；如果有，求出这个F′的值。

解：此时，m2的隔离方程将较为复杂。设绳子张力为T ，m2的受力情况如图，隔离方程为：

 = m2a

隔离m1 ，仍有：T = m1a

解以上两式，可得：a = g

最后用整体法解F即可。

答：当m1 ≤ m2时，没有适应题意的F′；当m1 ＞ m2时，适应题意的F′=  。

3、一根质量为M的木棒，上端用细绳系在天花板上，棒上有一质量为m的猫，如图17所示。现将系木棒的绳子剪断，同时猫相对棒往上爬，但要求猫对地的高度不变，则棒的加速度将是多少？

解说：法一，隔离法。需要设出猫爪抓棒的力f ，然后列猫的平衡方程和棒的动力学方程，解方程组即可。

法二，“新整体法”。

据Σ= m1 + m2 + m3 + … + mn ，猫和棒的系统外力只有两者的重力，竖直向下，而猫的加速度a1 = 0 ，所以：

（ M + m ）g = m·0 + M a1 

解棒的加速度a1十分容易。

答案：g 。

四、特殊的连接体

当系统中各个体的加速度不相等时，经典的整体法不可用。如果各个体的加速度不在一条直线上，“新整体法”也将有一定的困难（矢量求和不易）。此时，我们回到隔离法，且要更加注意找各参量之间的联系。

解题思想：抓某个方向上加速度关系。方法：“微元法”先看位移关系，再推加速度关系。、

1、如图18所示，一质量为M 、倾角为θ的光滑斜面，放置在光滑的水平面上，另一个质量为m的滑块从斜面顶端释放，试求斜面的加速度。

解说：本题涉及两个物体，它们的加速度关系复杂，但在垂直斜面方向上，大小是相等的。对两者列隔离方程时，务必在这个方向上进行突破。

（学生活动）定型判断斜面的运动情况、滑块的运动情况。

位移矢量示意图如图19所示。根据运动学规律，加速度矢量a1和a2也具有这样的关系。

（学生活动）这两个加速度矢量有什么关系？

沿斜面方向、垂直斜面方向建x 、y坐标，可得：

a1y = a2y             ①

且：a1y = a2sinθ     ②

隔离滑块和斜面，受力图如图20所示。

对滑块，列y方向隔离方程，有：

mgcosθ- N = ma1y     ③

对斜面，仍沿合加速度a2方向列方程，有：

Nsinθ= Ma2          ④

解①②③④式即可得a2 。

答案：a2 =  。

（学生活动）思考：如何求a1的值？

解：a1y已可以通过解上面的方程组求出；a1x只要看滑块的受力图，列x方向的隔离方程即可，显然有mgsinθ= ma1x ，得:a1x = gsinθ 。最后据a1 = 求a1 。

答：a1 =  。

2、如图21所示，与水平面成θ角的AB棒上有一滑套C ，可以无摩擦地在棒上滑动，开始时与棒的A端相距b ，相对棒静止。当棒保持倾角θ不变地沿水平面匀加速运动，加速度为a（且a＞gtgθ）时，求滑套C从棒的A端滑出所经历的时间。

解说：这是一个比较特殊的“连接体问题”，寻求运动学参量的关系似乎比动力学分析更加重要。动力学方面，只需要隔离滑套C就行了。

（学生活动）思考：为什么题意要求a＞gtgθ？（联系本讲第二节第1题之“思考题”）

定性绘出符合题意的运动过程图，如图22所示：S表示棒的位移，S1表示滑套的位移。沿棒与垂直棒建直角坐标后，S1x表示S1在x方向上的分量。不难看出：

S1x + b = S cosθ                   ①

设全程时间为t ，则有：

S = at2                          ②

S1x = a1xt2                        ③

而隔离滑套，受力图如图23所示，显然：

mgsinθ= ma1x                       ④

解①②③④式即可。

答案：t = 

另解：如果引进动力学在非惯性系中的修正式 Σ+ * = m （注：*为惯性力），此题极简单。过程如下——

以棒为参照，隔离滑套，分析受力，如图24所示。

注意，滑套相对棒的加速度a相是沿棒向上的，故动力学方程为：

F*cosθ- mgsinθ= ma相            （1）

其中F* = ma                      （2）

而且，以棒为参照，滑套的相对位移S相就是b ，即：

b = S相 = a相 t2                 （3）

解（1）（2）（3）式就可以了。

第二讲 配套例题选讲

教材范本：龚霞玲主编《奥林匹克物理思维训练教材》，知识出版社，2002年8月第一版。

例题选讲针对“教材”第三章的部分例题和习题。

如图所示，在光滑水平面上放着长为L，质理量为M的长木板，在长木板左端放一质量为m的物块（可视为质点），开始物体和长木板均处于静止状态，物块和长木板间的接触是粗糙的.今对物块m施一水平向右的恒力F，物块与木板分离时木板的速度为.下列判断正确的是（    ）

    A．若只增大物块质量m，则相对滑动过程木板加速度不变，但分离时速度v变大

    B．若只增大物块质量m，则相对滑动过程木板加速度增大，但分离时速度v变大

    C．若只增大恒力F，则相对滑动过程木板的加速度增大，分离时v也变大

D．若只增大恒力F，则相对滑动过程木板的加速度不变，但分离时v变小

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网