题目内容
 甲、乙两物体从同一点开始沿着同一直线向着同一方向运动,它们的速度-时间图象如图所示,求:
甲、乙两物体从同一点开始沿着同一直线向着同一方向运动,它们的速度-时间图象如图所示,求:(1)二者的加速度
(2)乙追上甲之前二者的最大距离是多少?
分析:(1)由速度图象的斜率可直接求出加速度.
(2)根据速度大小关系,分析甲乙两物体间距离的变化.两图线的交点表示速度相等,两个物体间的距离最大.根据“面积”求解即可.
(2)根据速度大小关系,分析甲乙两物体间距离的变化.两图线的交点表示速度相等,两个物体间的距离最大.根据“面积”求解即可.
解答:解:由题意得:
(1)速度图象的斜率表示加速度.则
甲的加速度a甲=
=
=-1m/s2;
乙的加速度a乙=
=
=0.33m/s2;
(2)3s前,甲的速度大,两者距离增大;3s后乙的速度,两者距离减小,故t=3s时,二者速度相等时,甲乙相距最远,则
△xmax=x甲-x乙=
×(4+1)×3-
×1×3=6m
答:
(1)甲的加速度a甲=-1m/s2;乙的加速度a乙=0.33m/s2;
(2)乙追上甲之前二者的最大距离是6m.
(1)速度图象的斜率表示加速度.则
甲的加速度a甲=
| △v |
| △t |
| 1-4 |
| 3 |
乙的加速度a乙=
| △v |
| △t |
| 1 |
| 3 |
(2)3s前,甲的速度大,两者距离增大;3s后乙的速度,两者距离减小,故t=3s时,二者速度相等时,甲乙相距最远,则
△xmax=x甲-x乙=
| 1 |
| 2 |
| 1 |
| 2 |
答:
(1)甲的加速度a甲=-1m/s2;乙的加速度a乙=0.33m/s2;
(2)乙追上甲之前二者的最大距离是6m.
点评:根据速度分析物体的运动情况是基本能力.本题是匀加速运动追及匀速运动的问题,当两者速度相等时,相距最远.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
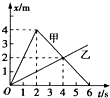 如图所示是甲、乙两物体从同一点出发的位移-时间(x-t)图象,由图象可以看出在0~4s这段时间内( )
如图所示是甲、乙两物体从同一点出发的位移-时间(x-t)图象,由图象可以看出在0~4s这段时间内( )| A、甲、乙两物体始终同向运动 | B、4 s时甲、乙两物体之间的距离最大 | C、甲的平均速度大于乙的平均速度 | D、甲、乙两物体之间的最大距离为3 m |
 甲、乙两物体从同一点开始做直线运动,其v-t图象如图所示,下列判断正确的是( )
甲、乙两物体从同一点开始做直线运动,其v-t图象如图所示,下列判断正确的是( )| A、在ta时刻两物体速度大小相等,方向相反 | B、在ta时刻两物体速度大小相等,方向相同 | C、在ta时刻两物体加速度大小相等,方向相同 | D、在ta时刻两物体加速度大小不等,方向相同 |
 如图是甲、乙两物体从同一点出发的运动图象,由图象可以看出在0到4秒内( )
如图是甲、乙两物体从同一点出发的运动图象,由图象可以看出在0到4秒内( ) 甲、乙两物体从同一点开始做直线运动,其v-t图象如图所示,下列判断正确的是( )
甲、乙两物体从同一点开始做直线运动,其v-t图象如图所示,下列判断正确的是( )