题目内容
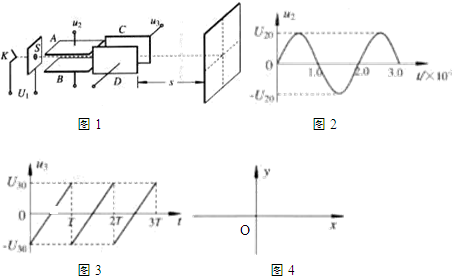
 两平行金属板间所加电压随时间变化的规律如图所示,大量质量为m、带电量为e的电子由静止开始经电压为U0的电场加速后连续不断地沿两平行金属板间的中线射入,若两板间距恰能使所有子都能通过.且两极长度使每个电子通过两板均历时3t0,电子所受重力不计,试求:
两平行金属板间所加电压随时间变化的规律如图所示,大量质量为m、带电量为e的电子由静止开始经电压为U0的电场加速后连续不断地沿两平行金属板间的中线射入,若两板间距恰能使所有子都能通过.且两极长度使每个电子通过两板均历时3t0,电子所受重力不计,试求:(1)电子通过两板时侧向位移的最大值和最小值;
(2)侧向位移最大和最小的电子通过两板后的动能之比.
分析:(1)根据在不同时段的运动性质,结合位移表达式,从而列出最大位移与最小位移关系式,即可求解;
(2)根据各自位移的不同,结合动能定理,即可求解.
(2)根据各自位移的不同,结合动能定理,即可求解.
解答:解:(1)电子在t=2 nt0(其中:n=0、1、2、…)时刻进入电场,电子通过两极的侧向位移最大,
在t=(2n+l)t0(其中n=0、l、2、…)时刻进入电场电子通过两板侧向位移最小.
电子侧向位移最大时,进入电场在沿电场线方向上作初速度为零的匀加速运动,
再作匀速运动,后作初速度不为零的匀加速运动,各段运动的时间均为t0;
当电子侧向位移最小时,在电场线上只有在第二个t0的时间开始作初速度为零的匀加速运动,
在第三个t0的时间作匀速运动.电子进入偏转电场后,在电场中的加速度均为a=
,电子侧向最大位移为
ymax=
at02+at02+at02+
at02=3at02=
.
解得:ymax=
由以上两式解得ymax=t0
;
d=2ymax=2t0
;
电子侧向最小位移为ymin=at02/2+at02=
ymax=
t0
;
解得:ymin=
(2)电子离开偏转电场时的动能等于加速电场和偏转电场电场力做功之和.
当电子的侧向位移为最大时,电子在电场中加速(只有加速,电场力才做功).
运动的距离为y1=
ymax=
,电子的侧向位移最小时,
电子在电场中加速运动的距离为y2=
ymin=
,
侧向位移最大的电子动能为 Ekmax=eUO+eUO?
=
eUO,
侧向位移最小的电子动能为Ekmin=eUO+eUO?
=
eUO,
故Ekmax:Ekmin=16:13
答:(1)电子通过两板时侧向位移的最大值
和最小值
;
(2)侧向位移最大和最小的电子通过两板后的动能之比16:13.
在t=(2n+l)t0(其中n=0、l、2、…)时刻进入电场电子通过两板侧向位移最小.
电子侧向位移最大时,进入电场在沿电场线方向上作初速度为零的匀加速运动,
再作匀速运动,后作初速度不为零的匀加速运动,各段运动的时间均为t0;
当电子侧向位移最小时,在电场线上只有在第二个t0的时间开始作初速度为零的匀加速运动,
在第三个t0的时间作匀速运动.电子进入偏转电场后,在电场中的加速度均为a=
| eU0 |
| md |
ymax=
| 1 |
| 2 |
| 1 |
| 2 |
3eU0
| ||
| md |
解得:ymax=
| d |
| 2 |
由以上两式解得ymax=t0
| ||
| m |
d=2ymax=2t0
| ||
| m |
电子侧向最小位移为ymin=at02/2+at02=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| m |
解得:ymin=
| d |
| 4 |
(2)电子离开偏转电场时的动能等于加速电场和偏转电场电场力做功之和.
当电子的侧向位移为最大时,电子在电场中加速(只有加速,电场力才做功).
运动的距离为y1=
| 2 |
| 3 |
| d |
| 3 |
电子在电场中加速运动的距离为y2=
| 1 |
| 3 |
| d |
| 12 |
侧向位移最大的电子动能为 Ekmax=eUO+eUO?
| y1 |
| d |
| 4 |
| 3 |
侧向位移最小的电子动能为Ekmin=eUO+eUO?
| y2 |
| d |
| 13 |
| 12 |
故Ekmax:Ekmin=16:13
答:(1)电子通过两板时侧向位移的最大值
| d |
| 2 |
| d |
| 4 |
(2)侧向位移最大和最小的电子通过两板后的动能之比16:13.
点评:考查由运动情况来运用位移与时间关系式,并掌握动能定理的应用,搞清不同时段的运动性质,这是解题的关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
 如图所示,水平放置的平行金属板M、N间距离为d,板长为l,在M、N间加上电压,M板的电势高于N板电势,质量为m 带电量为q的带正电粒子,以初速度v0平行金属板从两板正中间进入平行板间,带点粒子离开平行金属板后进入金属板右侧有直角三角形边界的匀强磁场区域,已知磁场区域AB边长为a,BC边水平,∠B=60°,∠C=90°,磁场方向垂直纸面向里,设带电粒子恰好从AB边的中点D以垂直AB边的速度方向进入磁场区域,不计带电粒子的重力,求:
如图所示,水平放置的平行金属板M、N间距离为d,板长为l,在M、N间加上电压,M板的电势高于N板电势,质量为m 带电量为q的带正电粒子,以初速度v0平行金属板从两板正中间进入平行板间,带点粒子离开平行金属板后进入金属板右侧有直角三角形边界的匀强磁场区域,已知磁场区域AB边长为a,BC边水平,∠B=60°,∠C=90°,磁场方向垂直纸面向里,设带电粒子恰好从AB边的中点D以垂直AB边的速度方向进入磁场区域,不计带电粒子的重力,求: 如图甲所示,A,B为两块平行金属板,板中央均有小孔,M、N是两块与B板垂直的平行金 属板,与M和N板等距离的中间轴线(图中虚线)通过0孔.M、N板长L=2X 1O -2m,板间距离d=4x10-3m,两板间所加电压U0=20V,在两板间形成匀强电场.一束电子 以初动能E0=120eV,从A板上的小孔0不断垂直于板射入A、B之间,现在A、B两板间 加一个如图乙所示的作周期性变化的电压U,在t=0到t=2s时间内A板电势高于B板 电势,则从t=0到t=4s的时间内.
如图甲所示,A,B为两块平行金属板,板中央均有小孔,M、N是两块与B板垂直的平行金 属板,与M和N板等距离的中间轴线(图中虚线)通过0孔.M、N板长L=2X 1O -2m,板间距离d=4x10-3m,两板间所加电压U0=20V,在两板间形成匀强电场.一束电子 以初动能E0=120eV,从A板上的小孔0不断垂直于板射入A、B之间,现在A、B两板间 加一个如图乙所示的作周期性变化的电压U,在t=0到t=2s时间内A板电势高于B板 电势,则从t=0到t=4s的时间内.