题目内容
18.已知月球绕地球公转的周期为T,轨道半径为r,万有引力常量为G,则由此求得的地球质量的表达式应为M地=$\frac{{4{π^2}{r^3}}}{{G{T^2}}}$.分析 根据万有引力提供向心力$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r,化简可得地球的质量.
解答 解:已知月球绕地球公转的周期为T,轨道半径为r,万有引力常量为G,根据万有引力提供向心力,有:
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r,
解得:M=$\frac{{4{π^2}{r^3}}}{{G{T^2}}}$
故答案为:$\frac{{4{π^2}{r^3}}}{{G{T^2}}}$
点评 本题要掌握万有引力提供向心力这个关系,选择恰当的向心力的表达式,计算中心天体的质量.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
6. 两个质量不同的物块A和B,分别从高度相同的光滑斜面和弧形曲面的顶点滑向底部,如下图所示.它们的初速度都为零,则下列说法正确的是( )
两个质量不同的物块A和B,分别从高度相同的光滑斜面和弧形曲面的顶点滑向底部,如下图所示.它们的初速度都为零,则下列说法正确的是( )
 两个质量不同的物块A和B,分别从高度相同的光滑斜面和弧形曲面的顶点滑向底部,如下图所示.它们的初速度都为零,则下列说法正确的是( )
两个质量不同的物块A和B,分别从高度相同的光滑斜面和弧形曲面的顶点滑向底部,如下图所示.它们的初速度都为零,则下列说法正确的是( )| A. | B下滑过程中重力所做的功比A下滑过程中重力所做的功多 | |
| B. | 它们达到底部时动能相等 | |
| C. | 它们达到底部时速率相等 | |
| D. | 物块A在最高点时的机械能和它到达最低点的机械能相等 |
13.以下关于自行车的许多部件的运动的描述正确的是( )
| A. | 前齿轮盘和后齿轮盘由于被同一条链条连接,所以线速度大小相等 | |
| B. | 后齿轮盘和脚踏板在同一个转轴上,所以角速度相同 | |
| C. | 如果前后轮半径相同则它们的线速度相同 | |
| D. | 如果前后轮半径不同则它们的线速度不同 |
3.下列关于匀速圆周运动中各物理量的关系表述正确的是( )
| A. | 由a=$\frac{{v}^{2}}{r}$可知,向心加速度总跟半径成反比 | |
| B. | 由a=vω可知,已知线速度与角速度大小可以求出向心加速度 | |
| C. | 线速度的计算公式为v=$\frac{2π}{T}$ | |
| D. | 线速度与角速度的关系为ω=vr |
8.如图所示的电路中,A1和A2是完全相同的灯泡,线圈L的电阻可以忽略,则( )


| A. | 合上开关S接通电路时,A2 先亮,A1后亮,最后一样亮 | |
| B. | 合上开关S接通电路时,A1和A2始终一样亮 | |
| C. | 断开开关S切断电路时,A2 立刻熄灭,A1过一会儿才熄灭 | |
| D. | 断开开关S切断电路时,A1和A2都要过一会儿才熄灭 |
 如图所示,质量为m=0.2kg的小球固定在长为L=0.9m的轻杆一端,杆可绕O点的水平转轴在竖直平面内转动.g=10m/s2,求:
如图所示,质量为m=0.2kg的小球固定在长为L=0.9m的轻杆一端,杆可绕O点的水平转轴在竖直平面内转动.g=10m/s2,求: 在xoy平面内,x轴的上方有匀强磁场,磁感应强度为B,方向如图所示,x轴的下方有匀强电场,电场强度为E,方向与y轴的正方向相反.今有电量为-q、质量为m的粒子(不计重力),从坐标原点沿y轴的正方向射出,射出以后,第三次到达x轴时,它与O点的距离为L,问:
在xoy平面内,x轴的上方有匀强磁场,磁感应强度为B,方向如图所示,x轴的下方有匀强电场,电场强度为E,方向与y轴的正方向相反.今有电量为-q、质量为m的粒子(不计重力),从坐标原点沿y轴的正方向射出,射出以后,第三次到达x轴时,它与O点的距离为L,问: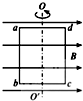 矩形线框abcd的边长分别为l1、l2,可绕它的一条对称轴OO′转动,线框电阻为R,转动角速度为ω.匀强磁场的磁感应强度为B,方向与OO′垂直,初位置时线圈平面与B平行,如图所示.
矩形线框abcd的边长分别为l1、l2,可绕它的一条对称轴OO′转动,线框电阻为R,转动角速度为ω.匀强磁场的磁感应强度为B,方向与OO′垂直,初位置时线圈平面与B平行,如图所示.