题目内容
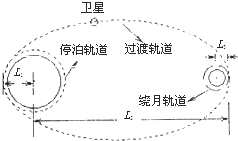我国发射的“嫦娥一号”卫星发射后首先进入绕地球运行的“停泊轨道”，通过加速再进入椭圆“过渡轨道”，该轨道离地心最近距离为L1，最远距离为L2，卫星快要到达月球时，依靠火箭的反向助推器减速，被月球引力“俘获”后，成为环月球卫星，最终在离月心距离L3的“绕月轨道”上飞行．已知地球半径为R，月球半径为r，地球表面重力加速度为g，月球表面的重力加速度为g/6，求：（1）卫星在“停泊轨道”上运行的周期，
（2）卫星在“绕月 轨道”上运行的线速度．
分析：（1）万有引力提供向心力G
=m(
)2L1，地球表面的物体受到的重力等于万有引力G
=mg，由以上二式可解得卫星在“停泊轨道”上运行的周期T．
（2）万有引力提供向心力G
=m
，在月球表面的物体受到的重力等于万有引力G
=mg月=
mg，由以上二式可解得卫星在“绕月轨道”上运行的线速度v2．
| M地m |
| L12 |
| 2π |
| T |
| M地m |
| R2 |
（2）万有引力提供向心力G
| M月m |
| L32 |
| v22 |
| L3 |
| M月m |
| r2 |
| 1 |
| 6 |
解答：解：（1）根据万有引力提供向心力G
=m(
)2L1
解得：T=2π
在地球表面的物体受到的重力等于万有引力G
=mg
得：GM地=R2g
所以T=2π
．
（2）根据万有引力提供向心力G
=m
解得v2=
在月球表面的物体受到的重力等于万有引力G
=mg月
得：GM月=r2g月=
gr2
所以v2=
．
答：（1）卫星在“停泊轨道”上运行的周期为2π
．
（2）卫星在“绕月轨道”上运行的线速度为
．
| M地m |
| L12 |
| 2π |
| T |
解得：T=2π
|
在地球表面的物体受到的重力等于万有引力G
| M地m |
| R2 |
得：GM地=R2g
所以T=2π
|
（2）根据万有引力提供向心力G
| M月m |
| L32 |
| v22 |
| L3 |
解得v2=
|
在月球表面的物体受到的重力等于万有引力G
| M月m |
| r2 |
得：GM月=r2g月=
| 1 |
| 6 |
所以v2=
|
答：（1）卫星在“停泊轨道”上运行的周期为2π
|
（2）卫星在“绕月轨道”上运行的线速度为
|
点评：本题要掌握天体运动的两个关系：万有引力提供向心力G
=m(
)2r，星球表面的物体受到的重力等于万有引力G
=mg．
| M m |
| r2 |
| 2π |
| T |
| M m |
| R2 |
练习册系列答案
考前必练系列答案
相关题目
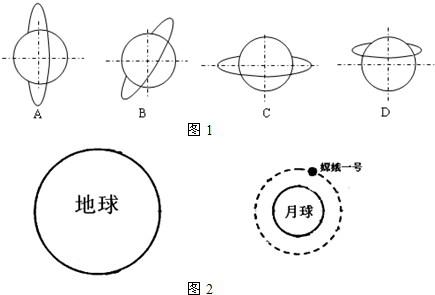
我国发射的“嫦娥一号”卫星绕月球经过一年多的运行，完成了既定任务，于2009年3月1日16时13分成功撞月．如图为“嫦娥一号”卫星撞月的模拟图，卫星在控制点1开始进入撞月轨道．假设卫星绕月球作圆周运动的轨道半径为R，周期为T，引力常量为G．根据题中信息，以下说法正确的是：（ ）
我国发射的“嫦娥一号”卫星经过多次加速、变轨后，最终成功进入环月工作轨道．如图所示，卫星既可以在离月球比较近的圆轨道a上运动，也可以在离月球比较远的圆轨道b上运动．下列说法正确的是（ ）
（2008?上海模拟）我国发射的“嫦娥一号”探月卫星简化后的路线示意图如图所示，卫星由地面发射后进入停泊轨道，在停泊轨道调速后进入地月转移轨道，再次调速后进入工作轨道，卫星开始对月球进行探测．已知地球与月球的质量之比为a，卫星相对地球的停泊轨道与卫星相对于月球的工作轨道的半径之比为b，卫星在停泊轨道和工作轨道上均可视为匀速圆周运动，则卫星在停泊轨道和工作轨道运行周期之比为
2010年10月1日18点59分57秒，我国在西昌卫星发射站发射了“嫦娥二号”，而我国发射的“嫦娥一号”卫星绕月球早已稳定运行，并完成了既定任务．“嫦娥二号”与“嫦娥一号”的最大不同在于“嫦娥二号”卫星是利用了大推力火箭直接被送到地月转移轨道，而“嫦娥一号”是送出地球后第三级火箭脱落．如图所示，为“嫦娥一号”在地月转移的轨道的一部分，从P向Q运动，直线MN是过O点且和两边轨迹相切，下列说法错误的是（ ）