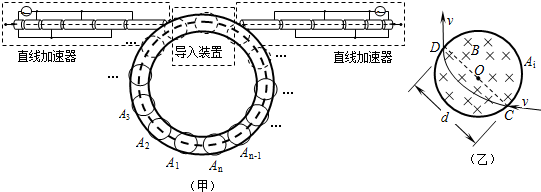
题目内容
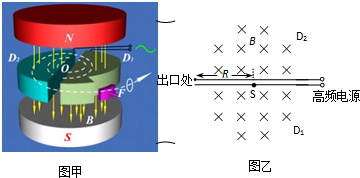
如图中甲所示,真空中两水平放置的平行金属板C、D,上面分别开有正对的小孔O1和O2,金属板C、D接在正弦交流电源上,C、D两板间的电压UCD随时间t变化的图线如图中乙所示.t=0时刻开始,从C板小孔O1处连续不断飘入质量为m=3.2×10-21kg、电荷量q=1.6×10-15C的带正电的粒子(设飘入速度很小,可视为零).在D板外侧有以MN为边界的匀强磁场,MN与金属板C相距d=10cm,匀强磁场的大小为B=0.1T,方向如图中所示,粒子的重力及粒子间相互作用力不计,平行金属板C、D之间的距离足够小,粒子在两板间的运动时间可忽略不计.求:(1)带电粒子经小孔O2进入磁场后,能飞出磁场边界MN的最小速度为多大?
(2)从0到0.04s末时间内哪些时刻飘入小孔O1的粒子能穿过电场并飞出磁场边界MN?
(3)以O2为原点建立直角坐标系,在图甲中画出粒子在有界磁场中可能出现的区域(用斜线标出),并标出该区域与磁场边界交点的坐标.要求写出相应的计算过程.

【答案】分析:(1)粒子在两板间的运动时间可忽略不计,可认为粒子通过电场的过程中认为板间电压不变.粒子在磁场做匀速圆周运动,轨迹与边界MN相切时,粒子恰好飞出MN,对应的速度最小.根据牛顿第二定律可求出最小速度.
(2)根据粒子能飞出磁场的最小速度,对粒子在电场中加速过程运用动能定理求出电压,分析电压图象,确定时间范围.
(3)当加速电压最大时,粒子在电场中获得的速度最大,进入磁场中圆周运动的半径最大,根据牛顿第二定律求出轨迹半径,由几何知识得到粒子飞出磁场相对小孔向左偏移的最小距离,即可得到磁场边界有粒子射出的长度范围.
解答: 解:(1)设带电粒子进入磁场后能飞出磁场边界的最小速度为V.
解:(1)设带电粒子进入磁场后能飞出磁场边界的最小速度为V.
粒子在磁场做匀速圆周运动,轨迹与边界MN相切时,粒子恰好飞出MN,对应的速度最小.
由几何知识得到此时轨迹半径为R=d
根据牛顿第二定律得:qVB=
∴V=5×103 m/s?
(2)设恰能飞出磁场边界MN的粒子在电场中运动时板D、C间对应电压为U,对于电场加速过程,
根据动能定理得:
qU= mv2
mv2
得 U=25 V
由图象可知,25 V电压对应的时刻分别为 秒和
秒和 秒,
秒,
故粒子能飞出磁场边界的时间为: 秒-
秒- 秒.
秒.
(3)设粒子的最大速度vm?
则 qνm= mvm2
mvm2
又qνmB=m
粒子飞出磁场相对小孔向左偏移的最小距离为x?
x=Rm- =0.04m
=0.04m
∴磁场边界有粒子射出的长度范围为△x=d-x=0.06m
答:
(1)带电粒子经小孔O2进入磁场后能飞出磁场边界的最小速度为5×103 m/s.?
(2)从0到0.04末的时间内, 秒-
秒- 秒时刻飘入小孔O1的粒子能穿过电场并飞出磁场边界.
秒时刻飘入小孔O1的粒子能穿过电场并飞出磁场边界.
(3)磁场边界有粒子射出的长度范围为0.06m,如图所示.
点评:粒子在磁场中圆周运动问题处理的基本方法是画轨迹,往往从分析边界情况,得到临界速度.常常用到几何和三角知识求解半径.
(2)根据粒子能飞出磁场的最小速度,对粒子在电场中加速过程运用动能定理求出电压,分析电压图象,确定时间范围.
(3)当加速电压最大时,粒子在电场中获得的速度最大,进入磁场中圆周运动的半径最大,根据牛顿第二定律求出轨迹半径,由几何知识得到粒子飞出磁场相对小孔向左偏移的最小距离,即可得到磁场边界有粒子射出的长度范围.
解答:
 解:(1)设带电粒子进入磁场后能飞出磁场边界的最小速度为V.
解:(1)设带电粒子进入磁场后能飞出磁场边界的最小速度为V.粒子在磁场做匀速圆周运动,轨迹与边界MN相切时,粒子恰好飞出MN,对应的速度最小.
由几何知识得到此时轨迹半径为R=d
根据牛顿第二定律得:qVB=

∴V=5×103 m/s?
(2)设恰能飞出磁场边界MN的粒子在电场中运动时板D、C间对应电压为U,对于电场加速过程,
根据动能定理得:
qU=
 mv2
mv2得 U=25 V
由图象可知,25 V电压对应的时刻分别为
 秒和
秒和 秒,
秒,故粒子能飞出磁场边界的时间为:
 秒-
秒- 秒.
秒.(3)设粒子的最大速度vm?
则 qνm=
 mvm2
mvm2又qνmB=m

粒子飞出磁场相对小孔向左偏移的最小距离为x?
x=Rm-
 =0.04m
=0.04m∴磁场边界有粒子射出的长度范围为△x=d-x=0.06m
答:
(1)带电粒子经小孔O2进入磁场后能飞出磁场边界的最小速度为5×103 m/s.?
(2)从0到0.04末的时间内,
 秒-
秒- 秒时刻飘入小孔O1的粒子能穿过电场并飞出磁场边界.
秒时刻飘入小孔O1的粒子能穿过电场并飞出磁场边界.(3)磁场边界有粒子射出的长度范围为0.06m,如图所示.
点评:粒子在磁场中圆周运动问题处理的基本方法是画轨迹,往往从分析边界情况,得到临界速度.常常用到几何和三角知识求解半径.

练习册系列答案
相关题目

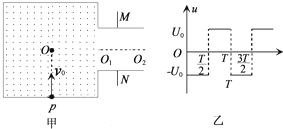 如图甲所示,在真空中,有一边长为a的正方形区域内存在匀强磁场,磁场方向垂直纸面向外.在磁场右侧有一对平行金属板M和N,两板间距及板长均为b,板间的中心线O1O2与正方形的中心O在同一直线上.有一电荷量为q、质量为m的带正电的粒子以速度v0从正方形的底边中点P沿PO方向进入磁场,从正方形右侧O1点水平飞出磁场时,立即给M、N两板加上如图乙所示的交变电压,最后粒子刚好以平行于M板的速度从M板的边缘飞出.(不计粒子所受到的重力、两板正对面之间为匀强电场,边缘电场不计)
如图甲所示,在真空中,有一边长为a的正方形区域内存在匀强磁场,磁场方向垂直纸面向外.在磁场右侧有一对平行金属板M和N,两板间距及板长均为b,板间的中心线O1O2与正方形的中心O在同一直线上.有一电荷量为q、质量为m的带正电的粒子以速度v0从正方形的底边中点P沿PO方向进入磁场,从正方形右侧O1点水平飞出磁场时,立即给M、N两板加上如图乙所示的交变电压,最后粒子刚好以平行于M板的速度从M板的边缘飞出.(不计粒子所受到的重力、两板正对面之间为匀强电场,边缘电场不计)