题目内容

精英家教网如图所示，在同一轨道平面上有A、B、C三颗人造地球卫星，它们各自的运转半径不相同，则下列关系正确的是（　　）
A、.三颗卫星的速度vA＜vB＜vCB、.三颗卫星所受向心力FA＞FB＞FCC、.三颗卫星的向心加速度aA＞aB＞aCD、.三颗卫星的周期TA＜TB＜TC
分析：研究卫星绕地球做匀速圆周运动，根据万有引力提供向心力，列出等式把要比较的物理量表示出来．根据已知条件结合表达式求解．
解答：解：A、根据万有引力提供向心力G
Mm
r2
=m
v2
r
，得v=
GM
r
，因为rA＜rB＜rC，所以vA＞vB＞vC，故A错误．
B、向心力等于万有引力F=G
Mm
r2
，由于不知道各个卫星的质量，故无法比较向心力的大小，故B错误．
C、根据万有引力提供向心力G
Mm
r2
=ma，得a=
GM
r2
，因为rA＜rB＜rC，所以aA＞aB＞aC，故C正确．
D、根据万有引力提供向心力G
Mm
r2
=m
4π2
T2
r，得T=2π
r3
GM
，因为rA＜rB＜rC，所以TA＜TB＜TC，故D正确．
故选：CD．
点评：比较一个物理量，我们应该把这个物理量先用已知的物理量表示出来，再根据表达式进行比较．向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用．
练习册系列答案
相关题目
（2012?泗县模拟）如图所示，在同一轨道平面上的几个人造星球卫星A、B、C，在某一时刻恰好在同一条直线上，下列说法中正确的是（　　）
如图所示，在同一轨道平面上的三颗不同的人造地球卫星，关于各物理量的关系，下列说法正确的是（　　）
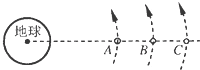精英家教网如图所示，在同一轨道平面上运行的3颗人造地球卫星A、B、C，在某一时刻恰好在同一直线上，下列说法中正确的是（　　）
A、根据v=
gr
，可知卫星在此时刻的速度vA＜vB＜vC
B、根据万有弓I力定律，卫星受到的万有引力FA＞FB＞FC
C、卫星的向心加速度aA＞aB＞aC
D、运动一周后，A先回到原地点
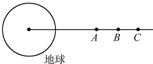精英家教网如图所示，在同一轨道平面上的几个质量不等的人造地球卫星A、B、C，均绕地球做匀速圆周运动，它们在某一时刻恰好在同一直线上，下列说法中正确的是（　　）
精英家教网如图所示，在同一轨道平面上，绕地球做圆周运动的卫星A、B和C，某时刻恰好在同一直线上，当卫星B运转一周时，下列说法正确的有（　　）
A、因为各卫星的角速度ωA=ωB=ωC，所以各卫星仍在原位置上B、因为各卫星运转周期TA＜TB＜TC，所以卫星A超前于卫星B，卫星C滞后于卫星BC、因为各卫星运转频率fA＞fB＞fC，所以卫星A滞后于卫星B，卫星C超前于卫星BD、因为各卫星的线速度vA＜vB＜vC，所以卫星A超前于卫星B，卫星C滞后于卫星B

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网