题目内容
如图所示，在同一轨道平面上的三颗不同的人造地球卫星，关于各物理量的关系，下列说法正确的是（ ）分析：人造卫星的运动都可近似看成匀速圆周运动，其向心力就是地球对它的万有引力F=G
，利用牛顿第二定律列方程分析．
| Mm |
| r2 |
解答：解：A、人造卫星的运动都可近似看成匀速圆周运动．由G
=m
有v=
，即卫星的线速度与轨道半径的平方根成反比，故A错误．
B、其向心力就是地球对它的万有引力F=G
，因质量关系未知，故B错误．
C、由G
=m（
）2r
有T=2π
，所以周期TA＜TB＜TC．故C正确
D、由G
=ma有a=G
，即卫星的向心加速度与轨道半径的平方成反比，故D错误
故选C．
| Mm |
| r2 |
| v2 |
| r |
有v=
|
B、其向心力就是地球对它的万有引力F=G
| Mm |
| r2 |
C、由G
| Mm |
| r2 |
| 2π |
| T |
有T=2π
|
D、由G
| Mm |
| r2 |
| M |
| r2 |
故选C．
点评：抓住万有引力提供向心力这一关系，灵活选择公式，整理出被求量表达式讨论一下即可
练习册系列答案
相关题目
（2012?泗县模拟）如图所示，在同一轨道平面上的几个人造星球卫星A、B、C，在某一时刻恰好在同一条直线上，下列说法中正确的是（ ）
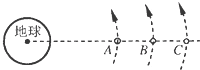如图所示，在同一轨道平面上运行的3颗人造地球卫星A、B、C，在某一时刻恰好在同一直线上，下列说法中正确的是（ ）A、根据v=
| ||
| B、根据万有弓I力定律，卫星受到的万有引力FA＞FB＞FC | ||
| C、卫星的向心加速度aA＞aB＞aC | ||
| D、运动一周后，A先回到原地点 |
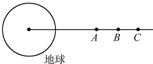如图所示，在同一轨道平面上，绕地球做圆周运动的卫星A、B和C，某时刻恰好在同一直线上，当卫星B运转一周时，下列说法正确的有（ ）| A、因为各卫星的角速度ωA=ωB=ωC，所以各卫星仍在原位置上 | B、因为各卫星运转周期TA＜TB＜TC，所以卫星A超前于卫星B，卫星C滞后于卫星B | C、因为各卫星运转频率fA＞fB＞fC，所以卫星A滞后于卫星B，卫星C超前于卫星B | D、因为各卫星的线速度vA＜vB＜vC，所以卫星A超前于卫星B，卫星C滞后于卫星B |