题目内容
如图所示，有一个正方形ABCD，E、F分别为BC和CD的中点，有一个小球从A点由静止开始沿着三个光滑斜面AC、AE、AF分别下滑到C、E、F三点，所用时间依次表示为t1、t2、t3，则（ ）
A．t1＞t2＞t3
B．t2＞t1＞t3
C．t3＞t1＞t2
D．以上判断均不正确
【答案】分析：根据几何关系求出斜面AC、AE、AF的长度，小球沿斜面AC、AE、AF做匀加速直线运动，根据受力情况求出加速度，再根据匀加速直线运动位移时间公式即可求出时间．
解答：解：设正方形的边长为l，斜面AC、AE、AF与AD的夹角分别为θ1、θ2、θ3，根据几何关系可知：AC=
、AE=AF=
，
根据牛顿第二定律得：
=5
m/s，
=
m/s，
=
小球沿斜面AC、AE、AF做匀加速直线运动，根据运动学基本公式得：
x=
解得：t=
所以
，
，
所以t3＞t1＞t2
故选C
点评：本题主要考查了牛顿第二定律及匀加速直线运动位移时间公式的直接应用，要比较某个量的关系，可以把这个物理量表示出来进行比较，难度适中．
解答：解：设正方形的边长为l，斜面AC、AE、AF与AD的夹角分别为θ1、θ2、θ3，根据几何关系可知：AC=
、AE=AF=，根据牛顿第二定律得：
=5m/s，=m/s，=小球沿斜面AC、AE、AF做匀加速直线运动，根据运动学基本公式得：
x=
解得：t=
所以
，，所以t3＞t1＞t2
故选C
点评：本题主要考查了牛顿第二定律及匀加速直线运动位移时间公式的直接应用，要比较某个量的关系，可以把这个物理量表示出来进行比较，难度适中．
练习册系列答案
相关题目
（2013?开封一模）如图所示，有一个等腰直角三角形的匀强磁场区域，其直角边长为L，磁场方向垂直纸面向外，磁感应强度大小为B．一边长为L总电阻为R的正方形导线框abcd，从图示位置开始沿x轴正方向以速度v匀速穿过磁 场区域．取沿a→b→c→d→a的感应电流为正，则表示线框中电流i随bC边的位置坐标x变化的图象正确的是（ ）
在直角坐标系xOy中，有一半径为R的圆形匀强磁场区域，磁感应强度为B，磁场方向垂直xOy平面指向纸面内，该区域的圆心坐标为（R，0），如图所示，有一个质量为m、带电荷量为-q的离子，由静止经电场加速后从点（0，
如图所示，有一个等腰直角三角形的匀强磁场区域，其直角边长为L，磁场方向垂直纸面向外，磁感应强度大小为B．边长为L、总电阻为R的正方形导线框abcd，从图示位置开始沿x轴正方向以速度v匀速穿过磁场区域．取沿a→b→c→d→a的感应电流为正，则下图中表示线框中电流i随bc边的位置坐标x变化的图象正确的是（ ）
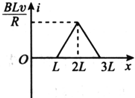
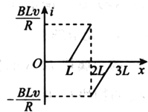
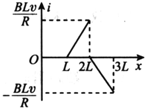
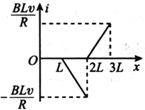
)越高
)越高