Question

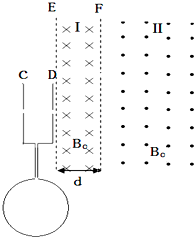（2013?惠州模拟）中心均开有小孔的金属板C、D与半径为d的圆形单匝金属线圈连接，圆形框内有垂直纸面的匀强磁场，大小随时间变化的关系为B=kt（k未知且k＞0），E、F为磁场边界，且与C、D板平行．D板右方分布磁场大小均为B₀，方向如图所示的匀强磁场．区域Ⅰ的磁场宽度为d，区域Ⅱ的磁场宽度足够大．在C板小孔附近有质量为m、电量为q的负离子由静止开始加速后，经D板小孔垂直进入磁场区域Ⅰ，不计离子重力．
（1）判断圆形线框内的磁场方向；
（2）若离子从C板出发，运动一段时间后又恰能回到C板出发点，求离子在磁场中运动的总时间；
（3）若改变圆形框内的磁感强度变化率k，离子可从距D板小孔为2d的点穿过E边界离开磁场，求圆形框内磁感强度的变化率k是多少？

Answer 1

分析：本题（1）的关键是根据楞次定律即可求解；题（2）的关键是画出离子运动的轨迹图，找出圆心，根据几何知识可求出三个轨迹对应的圆心角，即可求解；题（3）的关键是先根据法拉第电磁感应定律求出磁场变化率K，然后画出离子从距D板小孔为2d的点穿过E边界离开磁场时存在两种情况的轨迹图，根据几何知识求出圆的半径，代入即可求解．

解答：解：（1）负离子从C板向D板加速运动，说明D板电势高，对圆形电路，由楞次定律可知，感应电流方向应是逆时针，所以圆形线框内的磁场方向垂直纸面向里．  
（2）离子在Ⅰ、Ⅱ区域内作圆周运动，半径均为R，有：

qv   0 B

0

=

mv 2 0

R

…①
运动周期均为T，有：T=

2πR

v   0

…②
解①②得：T=

2πm

qB   0

… ③
由题意知粒子运动轨迹如图（甲），将三个轨迹的圆心连接起来，由几何知识可知，所得三角形为等边三角形，所以离子在磁场中运动的总时间为：t=2?

π 3

2π

?T+

2π- π 3

2π

?T=

T

3

+

5T

6

=

7T

6

…  ④
解③④得：t=

7πm

3q B   0

… ⑤

（3）单匝圆形线框产生的电动势为U，由法拉第电磁感应定律得：U=

S△B

△t

=K

πd

2

…⑥
离子从D板小孔射出速度为V，有动能定理得：qU=

1

2

mv

2

… ⑦
解①⑥⑦得：K=

qB 2 0     R 2

2π md 2

… ⑧
离子进入磁场从E边界射出的运动轨迹有两种情况：
（Ⅰ）如果离子从小孔下面离开磁场，运动轨迹与F相切，如图（乙）所示
由几何关系知：R=d…⑨
解⑧⑨得：K=

qB 2 0

2πm

…⑩
（Ⅱ）如果离子从小孔上面离开磁场，如图（丙）所示
由几何关系知：(R+d

)

2

+(2d

)

2

=(2R

)

2

…（11）
解⑧（11）得：K=

25 qB 2 0

18πm

…（12）

答：（1）圆形线框内的磁场方向垂直纸面向里；
（2）离子在磁场中运动的总时间为t=

7πm

3q B   0

；
（3）圆形框内磁感强度的变化率k是

qB 2 0

2πm

或

25 qB 2 0

18πm

点评：遇到带电粒子在有界磁场中的运动问题，一般思路是“画轨迹、定圆心、求半径和圆心角，然后求解”．