题目内容
如图，长方体ABCD是折射率为1.5的玻璃砖，将其放在空气中，一束光以入射角θ射到AB面的P点上，AD=2AP，求：
（1）要使此光束进入长方体后能直接折射到AD面上，θ的最小值是多少；
（2）要使此光束直接折射到AD面上的光能在AD面上发生全反射，θ的取值范围是多少．
（1）要使此光束进入长方体后能直接折射到AD面上，θ的最小值是多少；
（2）要使此光束直接折射到AD面上的光能在AD面上发生全反射，θ的取值范围是多少．
（1）当光束进入长方体后能直接折射到AD面上D点时，θ值最小．设折射角为r，根据几何知识得到
sinr=
又由题，AD=2AP，代入解得，sinr=
由折射率公式得，n=
得到
sinθ=nsinr=
n=
得到θ的最小值为arcsin
．
（2）当此光束直接折射到AD面上的光能在AD面上恰好发生全反射时，光线在AD面的入射角恰好等于临界角C，
由几何知识得到，此时AB面上的折射角r′=90°-C
由n=
得，sinθ′=nsinr′=nsin（90°-C）=ncosC=n
又sinC=
代入得sinθ′=
=
得到θ′=arcsic
所以要使此光束直接折射到AD面上的光能在AD面上发生全反射，θ≤arcsic
．
而光线要射到AD面上，θ≥arcsin
，所以使此光束直接折射到AD面上的光能在AD面上发生全反射，θ的取值范围是arcsin
≤θ≤arcsic
．
答：
（1）要使此光束进入长方体后能直接折射到AD面上，θ的最小值是arcsin
；
（2）要使此光束直接折射到AD面上的光能在AD面上发生全反射，θ的取值范围是arcsin
≤θ≤arcsic
．
sinr=
| AP | ||
|
又由题，AD=2AP，代入解得，sinr=
| ||
| 5 |
由折射率公式得，n=
| sinθ |
| sinr |
sinθ=nsinr=
| ||
| 5 |
3
| ||
| 10 |
得到θ的最小值为arcsin
3
| ||
| 10 |
（2）当此光束直接折射到AD面上的光能在AD面上恰好发生全反射时，光线在AD面的入射角恰好等于临界角C，
由几何知识得到，此时AB面上的折射角r′=90°-C
由n=
| sinθ′ |
| sinr′ |
| 1-sin2C |
又sinC=
| 1 |
| n |
代入得sinθ′=
| n2-1 |
| 1.25 |
得到θ′=arcsic
| 1.25 |
所以要使此光束直接折射到AD面上的光能在AD面上发生全反射，θ≤arcsic
| 1.25 |
而光线要射到AD面上，θ≥arcsin
3
| ||
| 10 |
3
| ||
| 10 |
| 1.25 |
答：
（1）要使此光束进入长方体后能直接折射到AD面上，θ的最小值是arcsin
3
| ||
| 10 |
（2）要使此光束直接折射到AD面上的光能在AD面上发生全反射，θ的取值范围是arcsin
3
| ||
| 10 |
| 1.25 |
练习册系列答案
相关题目
如图所示，将一个折射率为n的透明长方体放在空气中，矩形ABCD是它的一个截面，一单色细光束入射到P点，入射角为θ．
如图，长方体ABCD是折射率为1.5的玻璃砖，将其放在空气中，一束光以入射角θ射到AB面的P点上，AD=2AP，求：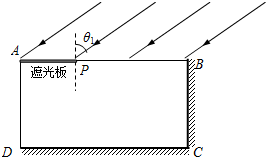
实验室有一块由透明介质组成的长方体，如图中ABCD所示．AB的长度为l1，AD的长度为l2，且AB和AD边透光，而BC和CD边不透光（射到这两个边的光线均被全部吸收）．现让一平行光束以入射角θ1射到AB面，经折射后 AD面上有光线射出．甲乙两同学分别用不同的方法测量该长方体介质的折射率．