题目内容
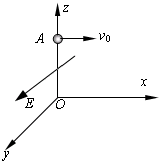
 如图所示,三维坐标系O-xOy的z轴方向竖直向上,所在空间存在y轴正方向的匀强电场,一质量为m、电荷量为+q的小球从z轴上的A点以速度v水平抛出,A点坐标为(0,0,l),重力加速度为g,场强E=
如图所示,三维坐标系O-xOy的z轴方向竖直向上,所在空间存在y轴正方向的匀强电场,一质量为m、电荷量为+q的小球从z轴上的A点以速度v水平抛出,A点坐标为(0,0,l),重力加速度为g,场强E=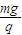 .下列说法中不正确的是( )
.下列说法中不正确的是( )A.小球做非匀变速曲线运动
B.小球运动的轨迹所在的平面与xOy平面的夹角为45°
C.小球的轨迹与xOy平面交点的坐标为(v
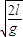 ,l,0)
,l,0)D.小球到达xOy平面时的速度大小为
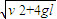
【答案】分析:根据小球受力情况可知小球所受合力不变,故小球做匀变速运动;由于初速度与加速度相互垂直,故小球在加速度与初速度构成的平面内做类平抛运动,其运动平面沿合外力方向;根据其轨迹所在的平面可知道轨迹与xoy平面的交点的y及z坐标,再根据沿z轴方向的运动规律求出小球运动的时间,从而求出小球沿x轴方向的位移即x轴坐标;根据运动时间及运动的加速度可求出小球到达xoy平面时沿合外力方向的速度最后根据速度的合成求出物体的合速度.
解答:解:A、小球在水平抛出后受力情况为:沿Z轴负方向的重力mg,沿y正方向的电场力qE=q×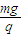 =mg,
=mg,
故小球所受的合力大小为F=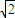 mg,
mg,
根据F=ma可得物体的加速度a=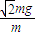 =
=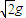 ,加速度a方向为y轴负方向偏z轴负方向45°,
,加速度a方向为y轴负方向偏z轴负方向45°,
故加速度方向与初速度方向不在同一条直线上,故物体做匀变速曲线运动.
故A错误.
B、由于小球的初速度v与加速度a所在的平面与xoy平面的夹角为45°,
故小球运动的轨迹所在的平面与xOy平面的夹角为45°,故B正确.
C、沿z轴负方向的位移为L在到达xoy平面前小球沿加速度方向通过的位移为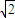 L,
L,
故其沿y轴方向的位移y=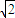 Lcos45°=L,
Lcos45°=L,
设小球到达xOy平面的时间t,
故有L=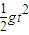 ,
,
所以t=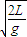 ,
,
沿x轴方向的位移x=vt=v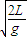 ,
,
故小球的轨迹与xOy平面交点的坐标为(v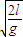 ,l,0),
,l,0),
故C正确.
D、小球沿加速度方向的速度v1=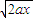 =
=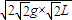 =2
=2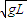
小球到达xOy平面时的速度大小为v=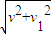 =
=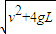 ,
,
故D正确.
本题选不正确的,故选A.
点评:类平抛运动和平抛运动遵循的规律类似,只是加速度不同,故要根据受力情况求出物体所受合外力,进而求出物体的加速度,再利用沿初速度方向做匀速直线运动,沿合外力方向做初速度为0的匀加速直线运动的规律来求解.
解答:解:A、小球在水平抛出后受力情况为:沿Z轴负方向的重力mg,沿y正方向的电场力qE=q×
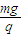 =mg,
=mg,故小球所受的合力大小为F=
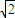 mg,
mg,根据F=ma可得物体的加速度a=
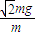 =
=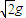 ,加速度a方向为y轴负方向偏z轴负方向45°,
,加速度a方向为y轴负方向偏z轴负方向45°,故加速度方向与初速度方向不在同一条直线上,故物体做匀变速曲线运动.
故A错误.
B、由于小球的初速度v与加速度a所在的平面与xoy平面的夹角为45°,
故小球运动的轨迹所在的平面与xOy平面的夹角为45°,故B正确.
C、沿z轴负方向的位移为L在到达xoy平面前小球沿加速度方向通过的位移为
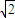 L,
L,故其沿y轴方向的位移y=
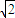 Lcos45°=L,
Lcos45°=L,设小球到达xOy平面的时间t,
故有L=
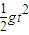 ,
,所以t=
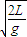 ,
,沿x轴方向的位移x=vt=v
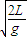 ,
,故小球的轨迹与xOy平面交点的坐标为(v
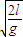 ,l,0),
,l,0),故C正确.
D、小球沿加速度方向的速度v1=
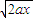 =
=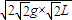 =2
=2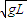
小球到达xOy平面时的速度大小为v=
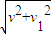 =
=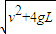 ,
,故D正确.
本题选不正确的,故选A.
点评:类平抛运动和平抛运动遵循的规律类似,只是加速度不同,故要根据受力情况求出物体所受合外力,进而求出物体的加速度,再利用沿初速度方向做匀速直线运动,沿合外力方向做初速度为0的匀加速直线运动的规律来求解.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
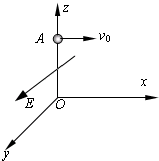 (2009?南通二模)如图所示,三维坐标系O-xyz的z轴方向竖直向上,所在空间存在y轴正方向的匀强电场,一质量为m、电荷量为+q的小球从z轴上的A点以速度v0水平抛出,A点坐标为(0,0,l),重力加速度为g,场强
(2009?南通二模)如图所示,三维坐标系O-xyz的z轴方向竖直向上,所在空间存在y轴正方向的匀强电场,一质量为m、电荷量为+q的小球从z轴上的A点以速度v0水平抛出,A点坐标为(0,0,l),重力加速度为g,场强 的
的 轴方向竖直向上,所在空间存在沿
轴方向竖直向上,所在空间存在沿 轴正方向的匀强电场。一质量为
轴正方向的匀强电场。一质量为 、电荷量为
、电荷量为 的小球从
的小球从 点以速度
点以速度 水平抛出,
水平抛出, ,
, ),重力加速度为
),重力加速度为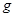 ,场强
,场强 。则下列说法中正确的是( )
。则下列说法中正确的是( )
 平面内的分运动为平抛运动
平面内的分运动为平抛运动 平面时的速度大小为
平面时的速度大小为
 ,
,
 ,l,0)
,l,0)