题目内容
一个实心圆柱导体和一个中空圆柱形导体共轴放置，其间为真空．实心柱体半径为a，中空柱体内半径为b，如图所示，其间有磁感应强度为B的匀强磁场，一个电子以径向速度从内柱体表面射出，试问电子的速度满足什么条件才能和中空柱体相碰，设电子质量为m，电量为e．
【答案】分析：电子在磁场中做匀速圆周运动，由牛顿第二定律及几何知识可得出电子能满足条件的速度．
解答：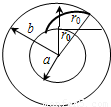
解：根据牛顿第二定律得：Bev=m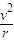
要电子和中空柱体相碰，至少是电子的轨迹与中空柱体相切，利用数学知识可求得最小半径r满足：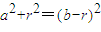
因为r＞r，
所以有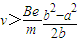
．
答：电子的速度满足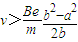
条件时才能和中空柱体相碰．
点评：解决带电粒子在磁场中的运动类题目，要能够正确的确定圆心和半径，利用好几何关系进行求解．
解答：
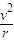
解：根据牛顿第二定律得：Bev=m要电子和中空柱体相碰，至少是电子的轨迹与中空柱体相切，利用数学知识可求得最小半径r满足：
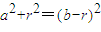
因为r＞r，
所以有
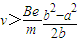． 答：电子的速度满足
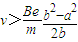条件时才能和中空柱体相碰．点评：解决带电粒子在磁场中的运动类题目，要能够正确的确定圆心和半径，利用好几何关系进行求解．
练习册系列答案
名校课堂系列答案
相关题目
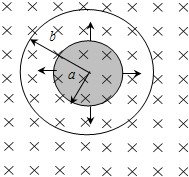（2005?南通模拟）一个实心圆柱导体和一个中空圆柱形导体共轴放置，其间为真空．实心柱体半径为a，中空柱体内半径为b，如图所示，其间有磁感应强度为B的匀强磁场，一个电子以径向速度从内柱体表面射出，试问电子的速度满足什么条件才能和中空柱体相碰，设电子质量为m，电量为e．一实心铁球和一实心木球质量相等，将它们放在同一水平面上，下列结论正确的是 ( )
| A．铁球的重力势能大于木球的重力势能 |
| B．铁球的重力势能等于木球的重力势能 |
| C．铁球的重力势能小于木球的重力势能 |
| D．上述三种情况都有可能 |
