Question

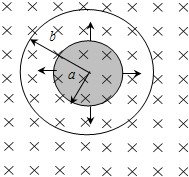（2005?南通模拟）一个实心圆柱导体和一个中空圆柱形导体共轴放置，其间为真空．实心柱体半径为a，中空柱体内半径为b，如图所示，其间有磁感应强度为B的匀强磁场，一个电子以径向速度从内柱体表面射出，试问电子的速度满足什么条件才能和中空柱体相碰，设电子质量为m，电量为e．

Answer 1

分析：电子在磁场中做匀速圆周运动，由牛顿第二定律及几何知识可得出电子能满足条件的速度．

解答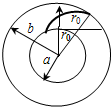：解：根据牛顿第二定律得：Bev=m

v2

r

要电子和中空柱体相碰，至少是电子的轨迹与中空柱体相切，利用数学知识可求得最小半径r₀满足：a2+r02=(b-r0)2
因为r＞r₀，
所以有v＞

Be

m

b2-a2

2b

． 
答：电子的速度满足v＞

Be

m

b2-a2

2b

条件时才能和中空柱体相碰．

点评：解决带电粒子在磁场中的运动类题目，要能够正确的确定圆心和半径，利用好几何关系进行求解．