题目内容
如图所示，两段光滑圆弧轨道半径分别为R1和R2，圆心分别为O1和O2，所对应的圆心角均小于5°，在最低点O平滑连接．M点和N点分别位于O点左右两侧，距离MO小于NO．现分别将位于M点和N点的两个小球A和B（均可视为质点）同时由静止释放．关于两小球第一次相遇点的位置，下列判断正确的是（ ）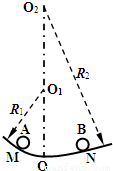
A．恰好在O点
B．一定在O点的左侧
C．一定在O点的右侧
D．条件不足，无法确定
【答案】分析：由题，两段光滑圆弧所对应的圆心角均小于5°，把两球在圆弧上的运动看做等效单摆运动，根据单摆的周期公式，分析两小球第一次到达O点的时间关系，即可判断第一次相遇的位置．
解答：解：据题意，两段光滑圆弧所对应的圆心角均小于5°，把两球在圆弧上的运动看做等效单摆，等效摆长等于圆弧的半径，则M、N两球的运动周期分别为
TM=2π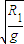
，TN=2π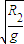
两球第一次到达O点的时间分别为
tM=
TM=
，tN=
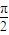
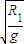TN=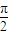
，
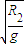由于R1＜R2，则 tM＜tN，故两小球第一次相遇点的位置一定在O点的右侧．
故选C
点评：本题关键是采用等效法，将两球在圆弧上的运动看做等效单摆运动，常常称为槽摆，再根据单摆的周期公式，比较时间，即可判断第一次相遇的位置．
解答：解：据题意，两段光滑圆弧所对应的圆心角均小于5°，把两球在圆弧上的运动看做等效单摆，等效摆长等于圆弧的半径，则M、N两球的运动周期分别为
TM=2π
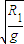，TN=2π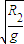两球第一次到达O点的时间分别为
tM=
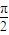
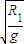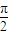
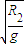TM=，tN=TN=，由于R1＜R2，则 tM＜tN，故两小球第一次相遇点的位置一定在O点的右侧．
故选C
点评：本题关键是采用等效法，将两球在圆弧上的运动看做等效单摆运动，常常称为槽摆，再根据单摆的周期公式，比较时间，即可判断第一次相遇的位置．
练习册系列答案
阅读快车系列答案
相关题目
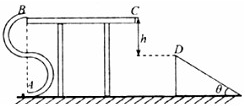如图所示，用内壁光滑的薄壁细管弯成的“S”形轨道固定于竖直平面内，其弯曲部分是由两个半径均为R=0.2m 的半圆平滑对接而成（圆的半径远大于细管内径）．轨道底端A与水平地面相切，顶端与一个长为l=0.9m的水平轨道相切B点．一倾角为θ=37°的倾斜轨道固定于右侧地面上，其顶点D与水平轨道的高度差为h=0.45m，并与其它两个轨道处于同一竖直平面内．一质量为m=0.1kg 的小物体（可视为质点）在A点被弹射入“S”形轨道内，沿轨道ABC运动，并恰好从D点无碰撞地落到倾斜轨道上．小物体与BC段间的动摩擦因数μ=0.5． （不计空气阻力，g取10m/s2．sin37°=0.6，cos37°=0.8）
如图所示，两金属杆AB和CD长均为L，电阻均为R，质量分别为3m和m．用两根质量和电阻均可忽略的不可伸长的柔软导线将它们连成闭合回路，并悬挂在水平、光滑、不导电的圆棒两侧．在金属杆AB下方距离为h处有高度为H（H＞h）匀强磁场，磁感应强度大小为B，方向与回路平面垂直，此时，CD刚好处于磁场的下边界．现从静止开始释放金属杆AB，经过一段时间下落到磁场的上边界，加速度恰好为零，此后便进入磁场．求金属杆AB