题目内容
18. 一立方体透明物体横截面如图所示,底面BC和右侧面CD均镀银(图中
一立方体透明物体横截面如图所示,底面BC和右侧面CD均镀银(图中粗线),P、M、Q、N分别为AB边、BC边、CD边、AD边的中点,虚线在ABCD所在的平面内并与AB平行,虚线上有一点光源S,从S发出一条细光线射到P点时与PA的夹角成30°,经折射后直接射到M点,从透明物体的AD面上射出后刚好可以回到S点.试求:(计算中可能会用到$\sqrt{2}$=1.41,$\sqrt{6}$=2.45,sin15°=0.26)
(i)透明物体的折射率n;
(ii)若光在真空中的速度为c,正方形ABCD的边长为a,则光从S点发出后,经过多长时间射回S点?
分析 根据光的折射定律,结合几何关系,即可求解;
根据几何知识,结合光在透明物体中的速度公式v=$\frac{c}{n}$,从而即可求解.
解答 解:(i)根据题意作光路图,光线在P点发生折射时,入射角为60°,折射角为45°
因此透明物体的折射率n=$\frac{sin60°}{sin45°}$=$\frac{\sqrt{6}}{\sqrt{2}}$=1.23
(ii)连接PN,由几何关系可得,PN,PM,QN,QM的长均为$\frac{\sqrt{2}}{2}$a,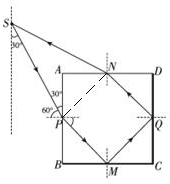
且∠PSN=30°,SN=SP=$\frac{\frac{PN}{2}}{sin15°}$
光在透明物体中的速度v=$\frac{c}{n}$
光透明物体中传播所用的时间t1=$\frac{PM+QM+QN}{v}$;
光在透明物体中传播所用的时间t2=$\frac{SP+SN}{c}$
那么光从S点发出射回到S点所经历的总时间为t=t1+t2=$\frac{5.33a}{c}$
答:(i)透明物体的折射率1.23;
(ii)若光在真空中的速度为c,正方形ABCD的边长为a,则光从S点发出后,经过$\frac{5.33a}{c}$时间射回S点.
点评 考查光的折射定律的应用,掌握传播速度与折射率的关系,注意正确的光路图是求解时间的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.关于速度、速度的变化量和加速度的关系,下列说法中正确的是( )
| A. | 速度变化量的方向为正,加速度的方向为负 | |
| B. | 物体加速度增大,速度一定越来越大 | |
| C. | 速度越来越大,加速度一定越来越大 | |
| D. | 速度变化越快,加速度越大 |
9. 某静电场中的一条电场线与x轴重合,其上电势的变化规律如图所示.在x0点由静止释放一负电荷,此电荷仅受电场力的作用,下列说法正确的是( )
某静电场中的一条电场线与x轴重合,其上电势的变化规律如图所示.在x0点由静止释放一负电荷,此电荷仅受电场力的作用,下列说法正确的是( )
 某静电场中的一条电场线与x轴重合,其上电势的变化规律如图所示.在x0点由静止释放一负电荷,此电荷仅受电场力的作用,下列说法正确的是( )
某静电场中的一条电场线与x轴重合,其上电势的变化规律如图所示.在x0点由静止释放一负电荷,此电荷仅受电场力的作用,下列说法正确的是( )| A. | 静电场是匀强电场 | |
| B. | 静电场是场强方向沿x轴负方向 | |
| C. | 电荷先沿x轴负方向做匀加速直线运动,然后做加速度减小的加速运动 | |
| D. | 电荷将沿x轴正方向做匀加速直线运动 |
6. 有一理想变压器,副线圈所接电路如图所示,灯L1、L2为规格相同的两只小灯泡.当S断开时,灯L1正常发光.S闭合后,下列说法正确的是( )
有一理想变压器,副线圈所接电路如图所示,灯L1、L2为规格相同的两只小灯泡.当S断开时,灯L1正常发光.S闭合后,下列说法正确的是( )
 有一理想变压器,副线圈所接电路如图所示,灯L1、L2为规格相同的两只小灯泡.当S断开时,灯L1正常发光.S闭合后,下列说法正确的是( )
有一理想变压器,副线圈所接电路如图所示,灯L1、L2为规格相同的两只小灯泡.当S断开时,灯L1正常发光.S闭合后,下列说法正确的是( )| A. | 灯L1、L2都能正常发光 | B. | 原线圈的输入功率减小 | ||
| C. | 原、副线圈的电流比增大 | D. | 电阻R消耗的功率增大 |
13. 如图所示,在一端封闭的光滑细玻璃管中注满清水,水中放一红蜡块R(R视为质点).将玻璃管的开口端用胶塞塞紧后竖直倒置且与y轴重合,R从坐标原点开始运动的轨迹如图所示,则红蜡块R在x、y方向的运动情况可能是( )
如图所示,在一端封闭的光滑细玻璃管中注满清水,水中放一红蜡块R(R视为质点).将玻璃管的开口端用胶塞塞紧后竖直倒置且与y轴重合,R从坐标原点开始运动的轨迹如图所示,则红蜡块R在x、y方向的运动情况可能是( )
 如图所示,在一端封闭的光滑细玻璃管中注满清水,水中放一红蜡块R(R视为质点).将玻璃管的开口端用胶塞塞紧后竖直倒置且与y轴重合,R从坐标原点开始运动的轨迹如图所示,则红蜡块R在x、y方向的运动情况可能是( )
如图所示,在一端封闭的光滑细玻璃管中注满清水,水中放一红蜡块R(R视为质点).将玻璃管的开口端用胶塞塞紧后竖直倒置且与y轴重合,R从坐标原点开始运动的轨迹如图所示,则红蜡块R在x、y方向的运动情况可能是( )| A. | x方向匀速直线运动,y方向匀速直线运动 | |
| B. | x方向匀速直线运动,y方向匀加速直线运动 | |
| C. | x方向匀减速直线运动,y方向匀加速直线运动 | |
| D. | x方向匀加速直线运动,y方向匀速直线运动 |
3. 如图所示,一物块置于水平地面上.当用与水平方向成30°角的力F1推物块时,物块做匀速直线运动;当改用与水平方向成60°角的力F2拉物块时,物块仍做匀速直线运动.若F2=F1,则物块与地面之间的动摩擦因数为( )
如图所示,一物块置于水平地面上.当用与水平方向成30°角的力F1推物块时,物块做匀速直线运动;当改用与水平方向成60°角的力F2拉物块时,物块仍做匀速直线运动.若F2=F1,则物块与地面之间的动摩擦因数为( )
 如图所示,一物块置于水平地面上.当用与水平方向成30°角的力F1推物块时,物块做匀速直线运动;当改用与水平方向成60°角的力F2拉物块时,物块仍做匀速直线运动.若F2=F1,则物块与地面之间的动摩擦因数为( )
如图所示,一物块置于水平地面上.当用与水平方向成30°角的力F1推物块时,物块做匀速直线运动;当改用与水平方向成60°角的力F2拉物块时,物块仍做匀速直线运动.若F2=F1,则物块与地面之间的动摩擦因数为( )| A. | $\frac{5\sqrt{3}}{2}-4$ | B. | 2-$\sqrt{3}$ | C. | 5$\sqrt{3}$-8 | D. | 1-$\frac{\sqrt{3}}{2}$ |

 如图,用一根绳子a把物体挂起来,再用另一根水平的绳子b把物体拉向一旁固定起来.物体的重力是40N,绳子a与竖直方向的夹角θ=37°,绳子a对物体的拉力大小为50N;若保持b绳水平,将悬点左移,增大角度θ,绳子a的拉力将会增大(填变大、变小或者不变).(sin37°=0.6,cos37°=0.8)
如图,用一根绳子a把物体挂起来,再用另一根水平的绳子b把物体拉向一旁固定起来.物体的重力是40N,绳子a与竖直方向的夹角θ=37°,绳子a对物体的拉力大小为50N;若保持b绳水平,将悬点左移,增大角度θ,绳子a的拉力将会增大(填变大、变小或者不变).(sin37°=0.6,cos37°=0.8)