题目内容
（12分）如图所示，绷紧的传送带，始终以v=2m/s的速度匀速斜向上运行，传送带与水平方向间的夹角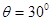
．现把质量m=10kg的工件轻轻地放在传送带底端P处，由传送带传送至顶端Q处．已知PQ之间的距离为4m，工件与传送带间的动摩擦因数为
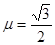，取g=10m/s2．
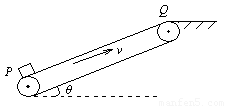
（1）通过计算说明工件在传送带上做什么运动；
（2）求工件从P点运动到Q点所用的时间．
【答案】
（1）工件在传送带上先做初速度为零、加速度为2.5m/s2的匀加速直线运动，后做匀速直线运动（2）2.4s
【解析】
试题分析：⑴当工件轻放于传送带上时，有：
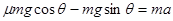得：
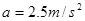（3分）
当其速度达到与传送带相等时，有：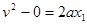
解得：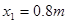
<
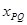，则随后工件沿传送带向上做匀速直线运动直至Q． （2分）
即工件在传送带上先做初速度为零、加速度为2.5m/s2的匀加速直线运动，后做匀速直线运动．
⑵对工件，设历时t1与传送带速度相等，有：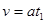
解得：
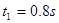（3分）
后做匀速直线运动，历时t2，有：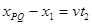
解得：
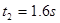（3分）
则工件由P至Q所用的时间ｔ为：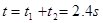
（1分）
即工件从P点运动到Q点所用的时间为2.4s
考点：考查牛顿第二定律的应用
点评：难度中等，处理传送带问题时，要根据工件与传送带的相对运动判断摩擦力方向，由牛顿第二定律求出加速度大小，转化为运动学问题求解
练习册系列答案
相关题目
（2010?越秀区三模）如图所示，绷紧的传送带与水平面的夹角θ=30°，皮带在电动机的带动下，始终保持v0=2m/s的速率运行．现把一质量m=10kg的工件（可看做质点）轻轻放在皮带的底端，经时间t=1.9s，工件被传送到h=1.5m的高处，取g=10m/s2．求：
如图所示，绷紧的传送带与水平而的夹角θ=30°，皮带在电动机的带动下，始终保持v=2m/s的速率运行．现把m=10kg的工件（可看作质点）轻轻放在皮带的底端，经时间1.9s，工件被传送到h=1.5m的高处，取g=10m/s2．求工件与皮带间的动摩擦因数．
如图所示，绷紧的传送带与水平面的夹角θ=30°，皮带在电动机的带动下，始终保持v0=2.5m/s的速率运行．将一质量m=1kg的工件（可看为质点）轻轻放在皮带的底端A点，工件能被传送到顶端B点，h=2.5m．已知工件与皮带间的动摩擦因数μ=
如图所示，绷紧的传送带与水平面的夹角θ=30°，传送带在电动机的带动下，始终保持v0=2m/s的速率运行．现把一质量为m=1kg的工件（可看为质点）轻轻放在传送带的底端，经时间t=1.9s，工件被传送到h=1.5m的高处，并取得了与传送带相同的速度，取g=10m/s2．求：
如图所示，绷紧的传送带与水平面的夹角α=30°，皮带在电动机的带动下，始终保持v0=2m/s的速率运行．现把一质量m=10kg的工件（可视为质点）轻轻放在皮带的底端，工件将被传送到h=2m的高处．设工件与皮带间的动摩擦因数μ=