题目内容
如图所示，直线MN表示一条平直公路，甲、乙两辆汽车分别停在A、B两处，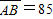
m，现甲车开始以a1=2.5m/s2的加速度向右做匀加速直线运动，当甲车运动t=6s时，乙车开始以a2=5m/s2的加速度向右做匀加速直线运动，求两车相遇处到A处的距离．
【答案】分析：首先根据甲车的加速度、初速度，求出t=6s时间内甲车的位移，判断是否追上了乙车．若没有追上乙车，根据相遇时两车之差等于AB间的距离求出相遇时间，再求解两车相遇处到A处的距离．
解答：解：甲车运动t=6s的位移为：
，
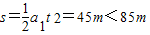说明t=6s甲车尚未追上乙车．
设此后甲车经过时间t与乙车相遇，
则有：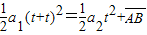
代入数据并整理得：t2-12t+32=0
解得：t1=4s t2=8s
（1）当t1=4s时，甲车追上乙车，第一次相遇处到A的距离为
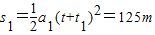
（2）当t2=8s时，乙车追上甲车，第二次相遇处到A的距离为
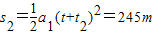
答：第一次相遇处到A的距离为125m，第二次相遇处到A的距离为245m．
点评：对于追及问题，除分别两个物体的运动情况外，关键是寻找它们之间的关系，比如时间关系、位移关系、速度关系等等．
解答：解：甲车运动t=6s的位移为：
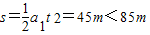，说明t=6s甲车尚未追上乙车．
设此后甲车经过时间t与乙车相遇，
则有：
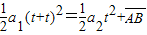
代入数据并整理得：t2-12t+32=0
解得：t1=4s t2=8s
（1）当t1=4s时，甲车追上乙车，第一次相遇处到A的距离为
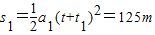
（2）当t2=8s时，乙车追上甲车，第二次相遇处到A的距离为
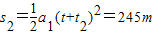
答：第一次相遇处到A的距离为125m，第二次相遇处到A的距离为245m．
点评：对于追及问题，除分别两个物体的运动情况外，关键是寻找它们之间的关系，比如时间关系、位移关系、速度关系等等．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
（2004?江苏）如图所示，U形导线框MNQP水平放置在磁感应强度B=0.2T的匀强磁场中，磁感线方向与导线框所在平面垂直，导线MN和PQ足够长，间距为0.5m，横跨在导线框上的导体棒ab的电阻r=1.0Ω，接在NQ间的电阻R=4．OΩ，电压表为理想电表，其余电阻不计．若导体棒在水平外力作用下以速度ν=2.0m/s向左做匀速直线运动，不计导体棒与导线框间的摩擦．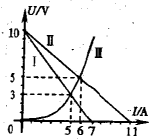
（1）如图所示，直线I、Ⅱ分别是电源1与电源2的路端电压随输出电流变化的图线，曲线Ⅲ是一个小灯泡的伏安特性曲线，则电源1和电源2的内阻之比为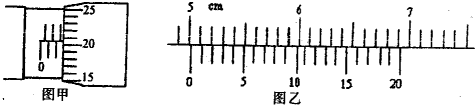
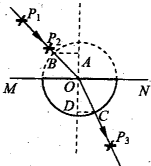示，某同学用插针法测定一半圆形玻璃砖的折射率，在平铺的白纸上垂直纸面插大头针P1、P2确定入射光线，
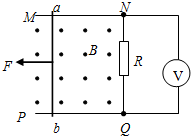如图所示，U形导线框MNQP水平放置在 磁感应强度B=0.2T的匀强磁场中，磁感线方向与导线框所在平面垂直，导线MN和PQ足够长，间距为L=0.5m，横跨在导线框上的导体棒ab的质量m=0.1kg，电阻r=1.0Ω，接在NQ间的电阻R=4.0Ω，电压表为理想电表，其余电阻不计．若导体棒在水平外力作用下以速度ν=2.0m/s向左做匀速直线运动，不计导体棒与导线框间的摩擦．求：
