题目内容
如图所示，轻杆长为3l，杆上距A球为l处的O点在水平转轴上，杆两端分别固定质量为m的A球和质量为3m的B球，杆在水平轴的带动下，在竖直平面内转动．问：
(1)若A球运动到最高点时，杆OA恰好不受力，求此时水平轴所受的力；
(2)在杆的转速逐渐增大的过程中，当杆转至竖直位置时，能否出现水平轴不受力的情况？如果出现这种情况，A、B两球的运动速度分别多大？
答案：略
解析：
解析：
|
(1)水平轴受竖直向下拉力，大小9mg； (2)能； A球在最高点恰好不受力，从这一点可以求出A球向心力情况，从而确定A球和B球的运动速度，进而利用这一观点判断第(2)问的可能性． (1)当A球运动到最高点时，杆OA恰好不受力，说明此时A球的重力恰好提供向心力，则有  ，可得 ．
又因为 A球与B球固定在同一杆上，因此 ．设此时OB杆对B球的拉力为F，则对B球有 ．代入可以求得F=9mg．
因为这时 A球对杆没有作用力，所以B球对杆的拉力大小也就等于杆对轴的作用力大小．由牛顿第三定律可知，杆对轴的拉力大小为9mg，方向竖直向下．(2)水平轴不受力，两段杆所受球的拉力大小一定相等，由牛顿第二定律：
由①－②得 
从上式可见，只有  时，③式才有意义，故 应为B球， 应为A球，已知条件代入③式，可得
∴ 
由以上分析可知，当杆处于竖直位置，月球在最高点，且  时，水平轴不受力，此时有：
|
．
练习册系列答案
相关题目
如图所示，轻杆长2l，中点装在水平轴O点，两端分别固定着小球A和B，A球质量为m，B球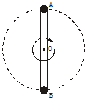
如图所示，轻杆长2l，中点装在水平轴O点，两端分别固定着小球A和B，A球质量为m，B球质量为2m，两者一起在竖直平面内绕O轴做圆周运动．
