题目内容
 如图所示,ACB为光滑圆弧轨道其半径为R,O为其圆心,OD为水平台面.AF为光滑水平面且与圆弧ACB光滑连接.已知:在DFAO区域存在水平向左的匀强电场,场强大小为E1,AOB右侧空间存在水平向右的匀强电场,场强大小为E2,且E1=E2.在AE水平面上有一个质量为m,电荷量为q的带负电小球(可看作质点).若其重力mg=qE1 问
如图所示,ACB为光滑圆弧轨道其半径为R,O为其圆心,OD为水平台面.AF为光滑水平面且与圆弧ACB光滑连接.已知:在DFAO区域存在水平向左的匀强电场,场强大小为E1,AOB右侧空间存在水平向右的匀强电场,场强大小为E2,且E1=E2.在AE水平面上有一个质量为m,电荷量为q的带负电小球(可看作质点).若其重力mg=qE1 问(1)至少从距离A点多远处无初速度释放该小球才能使其通过B点.(2)通过B点后落在水平面OD上距O点的距离在什么范围内.
分析:(1)要使小球到达B点,必须使小球通过AB上速度最小的点.由于mg=qE2,小球在圆弧轨道的等效最高点在OB右偏45°的H点上.在H点,由重力和电场力的合力恰好提供小球的向心力,由牛顿第二定律求得H点的速度,从小球释放到H点,再应用动能定理列式求解.
(2)从释放到B点的过程,运用动能定理列式求出小球到达B点的最小速度.小球离开B点做平抛运动,由平抛运动的规律求范围.
(2)从释放到B点的过程,运用动能定理列式求出小球到达B点的最小速度.小球离开B点做平抛运动,由平抛运动的规律求范围.
解答:解:(1)设至少从距离A点x1处无初速度释放该小球才能使其通过B点.
带电小球要通过B点,根据圆周运动规律,小球在圆弧轨道的等效最高点在OB右偏45°的H点上.从小球释放到H点,由动能定理得:
qE1x1-qE2
R-mg(1+
)R=
mv2
在H点,有
mg=m
又题意,mg=qE1=qE2.
联立以上三式得:x1=(1+
)R
(1)小球通过B点的速度为vB.由释放到B点,由动能定理得:
qE1x1-mg2R=
m
又mg=qE1.
解得,vB=
小球离开B点做平抛运动,由平抛运动的规律得:
R=
gt2
x2=vBt
解得,x2=
R
即通过B点后落在水平面OD上距O点的距离为x2≥
R.
答:
(1)至少从距离A点(1+
)R处无初速度释放该小球才能使其通过B点.
(2)通过B点后落在水平面OD上距O点的距离为x2≥
R.
带电小球要通过B点,根据圆周运动规律,小球在圆弧轨道的等效最高点在OB右偏45°的H点上.从小球释放到H点,由动能定理得:
qE1x1-qE2
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
在H点,有
| 2 |
| v2 |
| R |
又题意,mg=qE1=qE2.
联立以上三式得:x1=(1+
3
| ||
| 2 |
(1)小球通过B点的速度为vB.由释放到B点,由动能定理得:
qE1x1-mg2R=
| 1 |
| 2 |
| v | 2 B |
又mg=qE1.
解得,vB=
2(3
|
小球离开B点做平抛运动,由平抛运动的规律得:
R=
| 1 |
| 2 |
x2=vBt
解得,x2=
2(3
|
即通过B点后落在水平面OD上距O点的距离为x2≥
2(3
|
答:
(1)至少从距离A点(1+
3
| ||
| 2 |
(2)通过B点后落在水平面OD上距O点的距离为x2≥
2(3
|
点评:本题是动能定理与圆周运动临界条件、平抛运动的综合应用,关键是找到物理上的“最高点”H.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
如图所示,半圆形玻璃砖acb,O为圆心,c为圆弧顶点,一束很细的平行白光束沿cO方向射入玻璃砖,保持光的方向不变,而将玻璃砖沿顺时针方向绕O点转动,则首先在界面ab上发生全反射的应是白光中的( )
| A.红光成分,因为玻璃对红光折射率较大 |
| B.红光成分,因为玻璃对红光折射率较小 |
| C.紫光成分,因为玻璃对紫光折射率较大 |
| D.紫光成分,因为玻璃对红光折射率较小 |
 (2012?宝鸡模拟)如图所示,一直角三棱镜截面ABC,∠ABC=30°,∠ACB=90°斜边长为L,其折射率为n=
(2012?宝鸡模拟)如图所示,一直角三棱镜截面ABC,∠ABC=30°,∠ACB=90°斜边长为L,其折射率为n=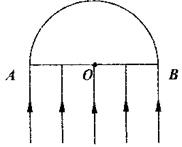 单色平行光a垂直射向一半径为R的玻璃半球的平面,其截面如图所示,发现半圆弧ACB上只有
单色平行光a垂直射向一半径为R的玻璃半球的平面,其截面如图所示,发现半圆弧ACB上只有 如图所示,一直角三棱镜面ABC,∠ABC=30°,∠ACB=90°,斜边长为L,其折射率为n=
如图所示,一直角三棱镜面ABC,∠ABC=30°,∠ACB=90°,斜边长为L,其折射率为n= ,一束平行光从斜边距A点
,一束平行光从斜边距A点 处的O点平行于BC边射入该棱镜。(光在真空中的速度c=3.0×108m/s,不考虑光的反射。)
处的O点平行于BC边射入该棱镜。(光在真空中的速度c=3.0×108m/s,不考虑光的反射。)