题目内容
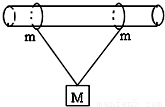如图所示，两个质量均为m的小环套在一水平放置的粗糙长杆上，两根长度均为l的轻绳一端系在小环上，另一端系在质量为M的木块上，两个小环之间的距离也为l，小环恰保持静止．试求：（1）小环对杆的压力；
（2）每根细线上的张力
（3）小环与杆之间的动摩擦因数μ至少为多大？（滑动摩擦力等于最大静摩擦力）
【答案】分析：木块被两根轻绳如图所示悬挂着处于平衡状态，而两环被两根绳子拉着也恰能保持静止．通过绳子的长度与两环的间距可以确定两绳的夹角，从而求出细线中的张力．再利用整体思想将每个小环对杆的压力算出，对于静摩擦力则是将绳子对环的拉力沿水平与竖直方向去分解，从而求出最大静摩擦力，由于滑动摩擦力等于最大静摩擦力，所以可借助于公式Ff=μFN求出动摩擦因数μ．
解答：解：（1）整体法分析有：2FN=（M+2m）g
即FN=
M g+mg
由牛顿第三定律得：小环对杆的压力FN′=
M g+mg
（2）研究M得 2FTcos30°=Mg
FT=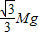
（3）环处于临界状态，此时小环受到的静摩擦力达到最大值，
则有：FTsin30°=μFN
解得：动摩擦因数μ至少为 μ=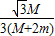
答：（1）小环对杆的压力
M g+mg
（2）每根细线上的张力=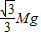
（3）小环与杆之间的动摩擦因数μ至少为=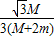
点评：本题需要对物体受力分析，由于两个物体，所以必须在选择研究对象．由于绳子拉环使得学生误解，杆对环的支持力的方向是与绳子方向相反，应该是与杆垂直．因为环刚好处于静止，所以此时所受摩擦力为最大值．
解答：解：（1）整体法分析有：2FN=（M+2m）g
即FN=
M g+mg 由牛顿第三定律得：小环对杆的压力FN′=
M g+mg （2）研究M得 2FTcos30°=Mg
FT=
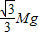
（3）环处于临界状态，此时小环受到的静摩擦力达到最大值，
则有：FTsin30°=μFN
解得：动摩擦因数μ至少为 μ=
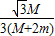
答：（1）小环对杆的压力
M g+mg （2）每根细线上的张力=
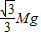
（3）小环与杆之间的动摩擦因数μ至少为=
点评：本题需要对物体受力分析，由于两个物体，所以必须在选择研究对象．由于绳子拉环使得学生误解，杆对环的支持力的方向是与绳子方向相反，应该是与杆垂直．因为环刚好处于静止，所以此时所受摩擦力为最大值．
练习册系列答案
相关题目
如图所示，两个质量均为m的小环套在一水平放置的粗糙长杆上，两根长度均为l的轻绳一端系在小环上，另一端系在质量为M的木块上，两个小环之间的距离也为l，小环保持静止．试求：
（2011?保定模拟）如图所示，两个质量均为m的物体A和B，由轻绳和轻弹簧连接绕过不计摩擦力的定滑轮，系统静止，将另一质量也是m的物体C，轻放在A上，在刚放上A的瞬间（ ）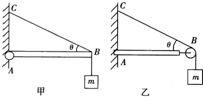
如图所示，两个质量均为m的物体分别挂在支架上的B点（如图甲所示）和跨过滑轮的轻绳BC上（如图乙所示），图甲中轻杆AB可绕A点转动，图乙中水平轻杆一端A插在墙壁内，已知θ=30°，则图甲中轻杆AB受到绳子的作用力F1和图乙中滑轮受到绳子的作用力F2分别为（ ）
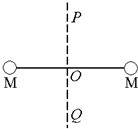如图所示，两个质量均为M的星体，O为两星体连线中点，PQ是其连线的垂直平分线，一个质量为m的物体从O沿OP方向一直运动下去，则它受到的万有引力大小变化情况是（ ）
（2005?广州模拟）如图所示，两个质量均为4m的小球A和B由轻弹簧连接，置于光滑水平面上．一颗质量为m子弹，以水平速度v0射入A球，并在极短时间内嵌在其中．求：在运动过程中