题目内容
某游乐场中有一种叫“空中飞椅”的游乐设施，其基本装置是将绳子上端固定在转盘的边缘上，绳子下端连接座椅，人坐在座椅上随转盘旋转而在空中飞旋．若将人和座椅看成是一个质点，则可简化为如图所示的物理模型．其中P为处于水平面内的转盘，可绕竖直转轴OO′转动，设绳长l=10m，质点的质量m=60kg，转盘静止时质点与转轴之间的距离d=4m．转盘逐渐转动起来，经过一段时间后质点与转盘一起做匀速圆周运动，此时绳与竖直方向的夹角θ=37°．（不计空气阻力及绳重，绳子不可伸长，sin37°=0.6，cos37°=0.8，g=10m/s2）求：质点与转盘一起做匀速圆周运动时转盘的角速度及绳子的拉力．分析：先结合几何关系质点圆周运动的半径．再根据合力提供向心力，由牛顿第二定律求出角速度和绳子拉力的大小．
解答：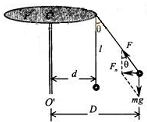
解：如图所示，对质点受力分析，由牛顿第二定律可得：
mgtanθ=mω2D
根据几何关系可得：D=d+lsinθ
代入数据得：ω=
rad/s=0.866rad/s
绳中的拉力T=
=
=750N
答：质点与转盘一起做匀速圆周运动时转盘的角速度是0.866rad/s，绳子的拉力是750N．
解：如图所示，对质点受力分析，由牛顿第二定律可得：mgtanθ=mω2D
根据几何关系可得：D=d+lsinθ
代入数据得：ω=
| ||
| 2 |
绳中的拉力T=
| mg |
| cosθ |
| 600 |
| 0.8 |
答：质点与转盘一起做匀速圆周运动时转盘的角速度是0.866rad/s，绳子的拉力是750N．
点评：本题关键要分析圆周运动向心力的来源，运用几何关系求圆周运动的半径．
练习册系列答案
相关题目
某游乐场中有一种叫“空中飞椅”的游乐设施，其基本装置是将绳子上端固定在转盘的边缘上，绳子下端连接座椅，人坐在座椅上随转盘旋转而在空中飞旋．若将人和座椅看成是一个质点，则可简化为如图所示的物理模型．其中P为处于水平面内的转盘，可绕竖直转轴OO′转动，设绳长l=10m，质点的质量m=60kg，转盘静止时质点与转轴之间的距离dd=4m．转盘逐渐加速转动，经过一段时间后质点与转盘一起做匀速圆周运动，此时绳与竖直方向的夹角θ=37°．（不计空气阻力及绳重，绳子不可伸长，sin37°=0.6，cos37°=0.8，g=10m/s2）求：
某游乐场中有一种叫“空中飞椅”的游乐设施，其基本装置是将绳子上端固定在转盘的边缘上，绳子下端连接座椅，人坐在座椅上随转盘旋转而在空中飞旋．若将人和座椅看成是一个质点，则可简化为如图的物理模型．其中P为处于水平面内的转盘，可绕竖直转轴OO′转动，设绳长l=10m，质点的质量m=60kg，转盘静止时质点与转轴之间的距离d=4m．转盘逐渐加速转动，经过一段时间后质点与转盘一起做匀速圆周运动，此时绳与竖直方向的夹角θ=370．（不计空气阻力及绳重，绳子不可伸长，sin37°=0.6，cos37°=0.8，g=10m/s2）求：
某游乐场中有一种叫“空中飞椅”的游乐设施，其基本装置是将绳子上端固定在转盘上，绳子下端连接座椅，人坐在飞椅上随转盘旋转而在空中飞旋．若将人与座椅看成质点，则可简化为如图所示的物理模型．其中P为处于水平面内的转盘，可绕竖直转轴OO′转动，设轻绳长L=10m，人与座椅的总质量m=60kg，转盘静止时人与转轴之间的距离d=4m，此时座椅离地面H=3m．转盘慢慢加速运动，经过一段时间后转速保持稳定，此时人与转轴之间的距离变为D=10m且保持不变．不计空气阻力，绳子不可伸长，取g=10m/s2．问：