题目内容
如图所示，细线的一端系一质量为m的小球，另一端固定在倾角为θ的光滑斜面体顶端，细线与斜面平行．在斜面体以加速度a水平向右做匀加速直线运动的过程中，小球始终静止在斜面上，重力加速度为g，小球受到细线的拉力为T，斜面的支持力为FN，则
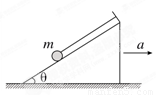
A．T＝m(g sinθ＋a cosθ)
B．T＝m(g cosθ＋a sinθ)
C．FN＝m(g cosθ－a sinθ)
D．FN＝m(g cosθ＋a sinθ)
【答案】
AC
【解析】
试题分析：当加速度a较小时，小球与斜面一起运动，此时小球受重力、绳子拉力和斜面的支持力，绳子平行于斜面；小球的受力如图：
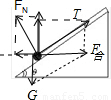
由牛顿第二定律得：Tcosθ-FNsinθ=ma ①
F合=mgcotθ=ma0
由平衡得：Tsinθ+FNcosθ=mg ②
①②联立得：FN=m（gcosθ-asinθ）
T=m（gsinθ+acosθ） 故AC正确，BD错误．故选AC．
考点：牛顿第二定律；力的合成与分解的运用．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
如图所示，细线的一端固定于倾角为45°的光滑楔形滑块A的顶端P处，细线的另一端拴一质量为m的小球．当细线对小球的拉力刚好等于零时，水平向右的加速度a的大小为（g为重力加速度）（ ）
（2013?琼海模拟）如图所示，细线的一端固定于O点，另一端系一小球．在水平拉力F作用下，小球以恒定速率在竖直平面内由A点运动到B点．在此过程中下列说法正确的是（ ）
（2013?静安区二模）如图所示，细线的一端固定于O点，另一端系一小球，在水平拉力F作用下，小球以恒定速率在竖直平面内由A点运动到B点的过程中（ ）
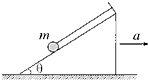如图所示，细线的一端系一质量为m的小球，另一端固定在倾角为θ的光滑斜面体顶端，细线与斜面平行．在斜面体以加速度a水平向右做匀加速直线运动的过程中，小球始终静止在斜面上，重力加速度为g，小球受到细线的拉力为T，斜面的支持力为FN，则（ ）| A、T=m（g sinθ+a cosθ） | B、T=m（g cosθ+a sinθ） | C、FN=m（g cosθ-a sinθ） | D、FN=m（g cosθ+a sinθ） |
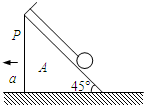如图所示，细线的一端固定于倾角为45°的光滑楔形滑块A的顶端P处，细线的另一端拴一质量为m的小球，当滑块至少以加速度a=