题目内容
17. 一列向右传播的横波在t=0时的波形如图所示,A、B两质点间距为8m,B、C两质点平衡位置的间距为3m,当t=1s时,质点C恰好通过平衡位置,该波的波速可能为( )
一列向右传播的横波在t=0时的波形如图所示,A、B两质点间距为8m,B、C两质点平衡位置的间距为3m,当t=1s时,质点C恰好通过平衡位置,该波的波速可能为( )| A. | $\frac{1}{3}$m/s | B. | 3m/s | C. | 5m/s | D. | 11m/s |
分析 根据图象可知:AB间距离等于一个波长λ.根据波形的平移法得到时间t=1s与周期的关系式,求出周期的通项,求出波速的通项,再得到波速的特殊值.
解答 解:由图读出波长λ=8m.
波向右传播,质点C恰好通过平衡位置时,波传播的最短距离为1m,根据波形的平移法得:t=(n+$\frac{1}{8}$)T或(n+$\frac{5}{8}$),n=0,1,2…,T=$\frac{8t}{8n+1}$s=$\frac{8}{8n+1}$s,
则波速v=$\frac{λ}{T}$=(8n+1)m/s 或v=(8n+5)
当n=0时:v=1m/s或5m/s,
当n=1时:v=9m/s或13m/s,
当n=2时:v=17m/s或21m/s,
故选:C
点评 本题的解题关键是运用波形平移法,得到时间与周期的关系式,得到波速的通项,再研究特殊值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列说法正确的是( )
| A. | 玛丽•居里首先提出原子的核式结构学说 | |
| B. | 卢瑟福在α粒子散射实验中发现了电子 | |
| C. | 查得威克在原子核人工转变的实验中发现了中子 | |
| D. | γ射线一般伴随着α或β射线产生,它的穿透能力最强 | |
| E. | γ射线在电场和磁场中都不会发生偏转 |
8. 如图1所示,是一个抽成真空的电子射线管,通电后管子左端的阴极能够发射电子.电子束从阴极向阳极运动,在通过图2示的磁场时将( )
如图1所示,是一个抽成真空的电子射线管,通电后管子左端的阴极能够发射电子.电子束从阴极向阳极运动,在通过图2示的磁场时将( )
 如图1所示,是一个抽成真空的电子射线管,通电后管子左端的阴极能够发射电子.电子束从阴极向阳极运动,在通过图2示的磁场时将( )
如图1所示,是一个抽成真空的电子射线管,通电后管子左端的阴极能够发射电子.电子束从阴极向阳极运动,在通过图2示的磁场时将( )| A. | 向上偏转 | B. | 向下偏转 | C. | 向N极偏转 | D. | 向S极偏转 |
5.汽车上坡的时候,司机必须换档,其目的是( )
| A. | 减小速度,得到较小的牵引力 | B. | 减小速度,得到较大牵引力 | ||
| C. | 增加速度,得到较小的牵引力 | D. | 增加速度,得到较大的牵引力 |
9.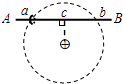 如图所示,光滑绝缘细杆AB水平置于被固定的带正电的可视为点电荷小球的正上方,小球的电荷量为Q.a、b是水平细杆上的两点,且在以带正电小球为圆心的同一竖直圆周上,c为a、b的中点.一个质量为m、电荷量为q的带负电的小圆环(可视为质点)套在细杆上,从a点由静止释放,在小圆环由a点运动到b点的过程中,下列说法中正确的是( )
如图所示,光滑绝缘细杆AB水平置于被固定的带正电的可视为点电荷小球的正上方,小球的电荷量为Q.a、b是水平细杆上的两点,且在以带正电小球为圆心的同一竖直圆周上,c为a、b的中点.一个质量为m、电荷量为q的带负电的小圆环(可视为质点)套在细杆上,从a点由静止释放,在小圆环由a点运动到b点的过程中,下列说法中正确的是( )
 如图所示,光滑绝缘细杆AB水平置于被固定的带正电的可视为点电荷小球的正上方,小球的电荷量为Q.a、b是水平细杆上的两点,且在以带正电小球为圆心的同一竖直圆周上,c为a、b的中点.一个质量为m、电荷量为q的带负电的小圆环(可视为质点)套在细杆上,从a点由静止释放,在小圆环由a点运动到b点的过程中,下列说法中正确的是( )
如图所示,光滑绝缘细杆AB水平置于被固定的带正电的可视为点电荷小球的正上方,小球的电荷量为Q.a、b是水平细杆上的两点,且在以带正电小球为圆心的同一竖直圆周上,c为a、b的中点.一个质量为m、电荷量为q的带负电的小圆环(可视为质点)套在细杆上,从a点由静止释放,在小圆环由a点运动到b点的过程中,下列说法中正确的是( )| A. | 小圆环在c点的加速度最大 | |
| B. | 小圆环在b点的动能最大 | |
| C. | 小圆环与带电小球组成的系统的电势能在c点最大 | |
| D. | 小圆环与带电小球组成的系统的电势能在b两点最大 |
7. 如图所示,长为2L的直导线AC折成边长相等,夹角为120°的V形,并置于与其所在平面相垂直的匀强磁场中,磁感应强度为B,当在该导线中通以电流强 度为I的电流时,该V形通电导线受到的安培力大小为( )
如图所示,长为2L的直导线AC折成边长相等,夹角为120°的V形,并置于与其所在平面相垂直的匀强磁场中,磁感应强度为B,当在该导线中通以电流强 度为I的电流时,该V形通电导线受到的安培力大小为( )
 如图所示,长为2L的直导线AC折成边长相等,夹角为120°的V形,并置于与其所在平面相垂直的匀强磁场中,磁感应强度为B,当在该导线中通以电流强 度为I的电流时,该V形通电导线受到的安培力大小为( )
如图所示,长为2L的直导线AC折成边长相等,夹角为120°的V形,并置于与其所在平面相垂直的匀强磁场中,磁感应强度为B,当在该导线中通以电流强 度为I的电流时,该V形通电导线受到的安培力大小为( )| A. | $\frac{1}{2}$BIL | B. | 2$\sqrt{3}$BIL | C. | $\sqrt{3}$BIL | D. | 2BIL |
 一物块以一定的初速度沿粗糙的斜面上滑,其上滑和下滑的速度大小随时间的变化关系如图所示,g=10m/s2.求:
一物块以一定的初速度沿粗糙的斜面上滑,其上滑和下滑的速度大小随时间的变化关系如图所示,g=10m/s2.求: 如图是光电门传感器,A为发光管,B为接收管,被测物体与遮光板相连,一旦光线被遮光板挡着,挡着的时间间隔能被光电门测出来.如图所示的小车上固定有遮光板,从静止开始做匀加速运动.实验测得遮光板的宽度d=3.0mm;遮光时间为2.0×10-3s;小车出发点距光电门的距离为s=55.5cm.则小车过光电门的速度为1.5m/s;小车的加速度为2.0m/s2(保留二位有效数字).
如图是光电门传感器,A为发光管,B为接收管,被测物体与遮光板相连,一旦光线被遮光板挡着,挡着的时间间隔能被光电门测出来.如图所示的小车上固定有遮光板,从静止开始做匀加速运动.实验测得遮光板的宽度d=3.0mm;遮光时间为2.0×10-3s;小车出发点距光电门的距离为s=55.5cm.则小车过光电门的速度为1.5m/s;小车的加速度为2.0m/s2(保留二位有效数字). 两块大小不同的圆形薄板(厚度不计),质量分别为M和m(M=2rn),半径分别为R和r,两板之间用一根长为L=0.4rm不可伸长的轻质绳相连结.开始时,两板水平叠放在支架C上方高h=0.2m处,支架上有一个半径为R′(r<R′<R)的圆孔,两板中心与圆孔中心在同一直线上,如图所示.现让两板一起自由下落,大圆板碰到支架后跳起,机械能无损失,小圆板穿过圆孔继续运动,两板分离,试求当细绳绷紧的瞬间两板的共同速度.(不计碰撞时间及空气阻力,取g=10m/s2)
两块大小不同的圆形薄板(厚度不计),质量分别为M和m(M=2rn),半径分别为R和r,两板之间用一根长为L=0.4rm不可伸长的轻质绳相连结.开始时,两板水平叠放在支架C上方高h=0.2m处,支架上有一个半径为R′(r<R′<R)的圆孔,两板中心与圆孔中心在同一直线上,如图所示.现让两板一起自由下落,大圆板碰到支架后跳起,机械能无损失,小圆板穿过圆孔继续运动,两板分离,试求当细绳绷紧的瞬间两板的共同速度.(不计碰撞时间及空气阻力,取g=10m/s2)