题目内容
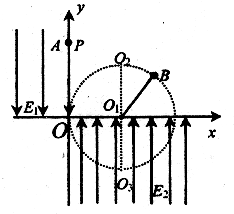 如图所示,竖直的xOy平面内,在x≤0、y≥0的区域内有电场强度E1=5×102N/C、方向竖直向下的匀强电场,x>0、y<0的区域内有电场强度为E2、方向竖直向上的匀强电场,E2=5El.不带电的小球B在xOy面内绕x轴上的O1点沿顺时针做圆周运动,运动到O点时速度大小vo=20m/s,带正电的小球A在y轴上纵坐标y1=0.4m的P点静止释放,恰好和B在O点发生正碰,并瞬间合成一个整体C,C能够经过最高点02和最低点03做圆周运动.A,B的质量都是m=0.1kg,拴小球B的轻质绝缘细绳长L=0.8m,A的电荷量q=2×10-3C.A、B、C都可以看作质点.g取10m/s2.求:
如图所示,竖直的xOy平面内,在x≤0、y≥0的区域内有电场强度E1=5×102N/C、方向竖直向下的匀强电场,x>0、y<0的区域内有电场强度为E2、方向竖直向上的匀强电场,E2=5El.不带电的小球B在xOy面内绕x轴上的O1点沿顺时针做圆周运动,运动到O点时速度大小vo=20m/s,带正电的小球A在y轴上纵坐标y1=0.4m的P点静止释放,恰好和B在O点发生正碰,并瞬间合成一个整体C,C能够经过最高点02和最低点03做圆周运动.A,B的质量都是m=0.1kg,拴小球B的轻质绝缘细绳长L=0.8m,A的电荷量q=2×10-3C.A、B、C都可以看作质点.g取10m/s2.求:(1)小球A下落到O点的速度v1是多大?
(2)C运动到03时,绳对C的拉力T是多大?
(3)小球A从y轴上y>0的某些位置开始下落,恰好在O点与B合成为C后,不能够做经过02和03的圆周运动.求这些位置的范围?
分析:(1)小球A下落到O点的过程中由动能定理即可求解;
(2)由动量守恒求得A与B碰后共同速度,再由动能定理结合向心力公式求解绳对C的拉力;
(3)C不能做能够经过O2和O3的圆周运动,即C不能达到能够经过O2和O3所需的最小速度.根据动量守恒定律、圆周运动向心力公式、动能定理联立方程即可求得范围.
(2)由动量守恒求得A与B碰后共同速度,再由动能定理结合向心力公式求解绳对C的拉力;
(3)C不能做能够经过O2和O3的圆周运动,即C不能达到能够经过O2和O3所需的最小速度.根据动量守恒定律、圆周运动向心力公式、动能定理联立方程即可求得范围.
解答:解:(1)由动能定理有(qE1+mg)y1=
mv12
解得v1=4m/s
(2)设A与B碰后共同速度为v2,以竖直向上为正方向,由动量守恒得
mv0-mv1=2mv2
解得v2=8m/s
设C运动到O3时速度v3,则
2mgL-qE2L=
×2mv32-
×2mv22
T+qE2-2mg=2m
解得T=7N
(3)C不能做能够经过O2和O3的圆周运动,即C不能达到能够经过O2和O3所需的最小速度.设C能够做经过O2的圆周运动,在O2所需的最小速度为v4,设C能够做经过O3的圆周运动,在O3所需的最小速度为v5,则
2mg=2m
qE2-2mg=2m
解得:v4=2
m/s,v5=2
m/s
C经过O3时速度为v5=2
m/s,设经过O2时速度为v6,则
2qE2L-4mgL=
×2mv62-
×2mv52,由于2qE2L-4mgL>0,所以v6>v5=2
m/s>v4=2
m/s.
即C能够做经过O3就一定能够做经过O2.
当C能够做经过O3的速度小于v5=2
m/s时,不能做能够经过O2和O3的圆周运动.
设C经过O3的速度为v5时,A与B碰后在O点的共同速度为v7,则
2mgL-qE2L=
×2mv52-
×2mv72
解得:v7=6m/s
C在O点的速度只要大小为v7,不管是向上还是向下,C都能够经过O3.
设C的速度向上时,碰前A的速度为v8,在y轴上开始位置的坐标为y2,则
mv0-mv8=2mv7
(qE1+mg)y2=
mv82
解得v8=8m/s,y2=1.6m
设C的速度向下时,碰前A的速度为v9,在y轴上开始位置的坐标为y3,则
mv0-mv9=-2mv7
(qE1+mg)y3=
mv92
解得v9=32m/s,y3=25.6m
即1.6m<y<25.6m时,C不能做能够经过O2和O3的圆周运动.
答:(1)小球A下落到O点的速度为4m/s;
(2)C运动到03时,绳对C的拉力T是7N;
(3)当1.6m<y<25.6m时,C不能做能够经过O2和O3的圆周运动.
| 1 |
| 2 |
解得v1=4m/s
(2)设A与B碰后共同速度为v2,以竖直向上为正方向,由动量守恒得
mv0-mv1=2mv2
解得v2=8m/s
设C运动到O3时速度v3,则
2mgL-qE2L=
| 1 |
| 2 |
| 1 |
| 2 |
T+qE2-2mg=2m
| v32 |
| L |
解得T=7N
(3)C不能做能够经过O2和O3的圆周运动,即C不能达到能够经过O2和O3所需的最小速度.设C能够做经过O2的圆周运动,在O2所需的最小速度为v4,设C能够做经过O3的圆周运动,在O3所需的最小速度为v5,则
2mg=2m
| v42 |
| L |
qE2-2mg=2m
| v52 |
| L |
解得:v4=2
| 2 |
| 3 |
C经过O3时速度为v5=2
| 3 |
2qE2L-4mgL=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
即C能够做经过O3就一定能够做经过O2.
当C能够做经过O3的速度小于v5=2
| 3 |
设C经过O3的速度为v5时,A与B碰后在O点的共同速度为v7,则
2mgL-qE2L=
| 1 |
| 2 |
| 1 |
| 2 |
解得:v7=6m/s
C在O点的速度只要大小为v7,不管是向上还是向下,C都能够经过O3.
设C的速度向上时,碰前A的速度为v8,在y轴上开始位置的坐标为y2,则
mv0-mv8=2mv7
(qE1+mg)y2=
| 1 |
| 2 |
解得v8=8m/s,y2=1.6m
设C的速度向下时,碰前A的速度为v9,在y轴上开始位置的坐标为y3,则
mv0-mv9=-2mv7
(qE1+mg)y3=
| 1 |
| 2 |
解得v9=32m/s,y3=25.6m
即1.6m<y<25.6m时,C不能做能够经过O2和O3的圆周运动.
答:(1)小球A下落到O点的速度为4m/s;
(2)C运动到03时,绳对C的拉力T是7N;
(3)当1.6m<y<25.6m时,C不能做能够经过O2和O3的圆周运动.
点评:本题主要考查了动量守恒、动能定理、向心力公式的应用,要求同学们能正确分析小球的运动情况,选择合适的定律求解,综合性较强,难度较大.

练习册系列答案
相关题目
 如图所示,水平导轨间距为L,左端接有阻值为R的定值电阻.在距左端xo处放置一根质量为m、电阻为r的导体棒,导体棒与导轨间无摩擦且始终保持良好接触,导轨的电阻可忽略,整个装置处在竖直向上的匀强磁场中.
如图所示,水平导轨间距为L,左端接有阻值为R的定值电阻.在距左端xo处放置一根质量为m、电阻为r的导体棒,导体棒与导轨间无摩擦且始终保持良好接触,导轨的电阻可忽略,整个装置处在竖直向上的匀强磁场中. (2011?泰州一模)如图所示,x0y平面内,y轴左侧有方向竖直向下,电场强度为E=1.0×104N/的匀强电场.在Y轴右侧有一个边界为圆形的匀强磁场区域,圆心O′位于x轴上,半径为r=0.01m,磁场最左边与Y轴相切于O点,磁感应强度为B=0.01T,方向垂直纸面向里.在坐标xo=0.06m处有垂直于x轴的足够大的荧光屏PQ.一束带正电的粒子从电场中的A点(图中未标出)以垂直于电场的初速度向右运动,穿出电场时恰好通过坐标原点,速度大小为v=2×106m/s,方向与x轴正向成300角斜向下.已知粒子的质量为m=1.0×l0-2kg,电量为q=1.0×10-10C,重力不计.
(2011?泰州一模)如图所示,x0y平面内,y轴左侧有方向竖直向下,电场强度为E=1.0×104N/的匀强电场.在Y轴右侧有一个边界为圆形的匀强磁场区域,圆心O′位于x轴上,半径为r=0.01m,磁场最左边与Y轴相切于O点,磁感应强度为B=0.01T,方向垂直纸面向里.在坐标xo=0.06m处有垂直于x轴的足够大的荧光屏PQ.一束带正电的粒子从电场中的A点(图中未标出)以垂直于电场的初速度向右运动,穿出电场时恰好通过坐标原点,速度大小为v=2×106m/s,方向与x轴正向成300角斜向下.已知粒子的质量为m=1.0×l0-2kg,电量为q=1.0×10-10C,重力不计. 如图所示,质量为m的尖劈A顶角α=37°,一面靠在竖直的光滑墙壁上,质量为2m的方木块B放在水平光滑地面上,A和B之间无摩擦,弹簧右端固定.方木块B将弹簧压缩xo后,由静止释放,A在B的推动下,沿竖直光滑的墙壁上滑,当弹簧刚恢复原长时,B的速度为vB.(重力加速度为g,sin37°=0.6)
如图所示,质量为m的尖劈A顶角α=37°,一面靠在竖直的光滑墙壁上,质量为2m的方木块B放在水平光滑地面上,A和B之间无摩擦,弹簧右端固定.方木块B将弹簧压缩xo后,由静止释放,A在B的推动下,沿竖直光滑的墙壁上滑,当弹簧刚恢复原长时,B的速度为vB.(重力加速度为g,sin37°=0.6) (2011?黄冈模拟)如图所示,粗糙绝缘水平面AB与半径足够大的光滑绝缘圆弧面BC平滑相接于B,BC弧的圆心O与β的连线和竖直方向成37°,水平面上方存在水平向右的匀强电场.在BC上的M点自由释放一个带正电的小滑块,滑块沿弧面滑到水平面上,最远能够到达距B为xo=0.4m的N点.此后,滑块又向右运动,越过B滑上圆弧面,到达最高处后又开始下滑…如此往复,最终停在B处.已知滑块质量m=l.2kg,与水平面之间的滑动摩擦因数μ=0.25,受到的电场力qE=
(2011?黄冈模拟)如图所示,粗糙绝缘水平面AB与半径足够大的光滑绝缘圆弧面BC平滑相接于B,BC弧的圆心O与β的连线和竖直方向成37°,水平面上方存在水平向右的匀强电场.在BC上的M点自由释放一个带正电的小滑块,滑块沿弧面滑到水平面上,最远能够到达距B为xo=0.4m的N点.此后,滑块又向右运动,越过B滑上圆弧面,到达最高处后又开始下滑…如此往复,最终停在B处.已知滑块质量m=l.2kg,与水平面之间的滑动摩擦因数μ=0.25,受到的电场力qE=