Question

如图所示，光滑水平面MN的左端M处有一弹射装置P，右端N处与水平传送带理想连接．传送带水平部分长L=8m，并以恒定速度v=3m/s沿图示箭头方向移动．质量均为m=1kg、静止于MN上的物块A、B（视为质点）之间压缩一轻弹簧，贮有弹性势能E_P=16J．若A、B与传送带间的动摩擦因数μ=0.2，则解除弹簧压缩，弹开物块A、B后，求：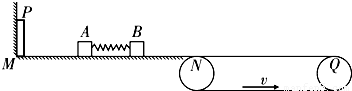
（1）物块B在传送带上向右滑行的最远距离L₁；
（2）物块B返回到水平面MN时的速度v_B′；
（3）若物块B返回水平面MN后，与被弹射装置P弹回的物块A在水平面MN上弹性碰撞（碰撞过程无动能损失，碰撞时间极短），使物块B从传送带水平部分的右端Q滑出，则弹射装置P必须给物块A至少做多少功？

Answer 1

【答案】分析：（1）A、B被弹簧弹开的过程实际是爆炸模型，符合动量守恒、系统机械能守恒，根据能量守恒和动量守恒求出分开后，A、B的速度大小，然后根据动能定理即可求出B沿传送带向右滑动的最远距离；
（2）物块B沿传送带向左返回时，若物块B加速到传送带速度v需要滑动的距离大于s_m，则物块一直加速，若小于s_m，则先加速后减速；
（3）B能从Q端滑出的条件是B到达后速度大于等于零，然后根据功能关系列方程可正确解答．
解答：解：（1）解除锁定后弹簧恢复原长时，A、B的速度大小分别为v_A、v_B，由系统机械能守恒、动量守恒得：
m_Bv_B=m_Av_A    
E=m_Bv_B²+m_Av_A²   
联立解得  v_A=v_B=4m/s
设B沿传送带向右滑行的最远距离为L₁，由功能关系  μmg L₁=mv_B²    
解得  L₁=4m   
（2）因为v=4m/s＞3m/s，所以B返回时先加速再随传送带一起运动，B返回到水平面MN时的速度
v_B′=3m/s   
（3）以A为研究对象，设碰后A、B的速度分别为v_A′、v_B″，由动能定理
W=m_Av_A′²-m_Av_A²  
B能从Q端滑出一定有  m_Bv_B″²≥μmgL   
A与B质量相等，完全弹性碰撞后速度互换，则A的速度v_A′=v_B″
联立解得  W≥8J．
答：（1）物块B在传送带上向右滑行的最远距离为4m；
（2）物块B返回到水平面MN时的速度为3m/s；
（3）弹射装置P必须给物块A至少做8J的功．
点评：该题是动量守恒，能量守恒综合应用的一道比较困难的题目，正确分析题目当中的临界条件是关键．