题目内容
用一根细绳,一端系住一定质量的小球,小球大小忽略.另一端固定在天花板上,使小球做如图的匀速圆周运动.现在有如图5两个这样的装置(a)和(b),(a)、(b)图中,两球转动的角速度大小相同,绳与竖直方向的夹角分别为37°和53°.则a、b两球的转动半径Ra和Rb之比,以及相对应的绳子的长度La和Lb之比分别为:(sin37°=0.6;cos37°=0.8)( )
A.Ra:Rb=9:16;La:Lb=4:3
B.Ra:Rb=9:16;La:Lb=3:4
C.Ra:Rb=3:4;La:Lb=9:16
D.Ra:Rb=3:4;La:Lb=16:9
【答案】分析:小球做圆周运动的向心力由绳子的拉力和重力的合力提供,根据牛顿第二定律求出角速度与半径的关系,从而得出转动半径之比,再根据几何关系得出绳长之比.
解答:解:小球所受的合力F合=mgtanθ=mrω2,则角速度的大小ω=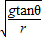 ,
,
由于角速度大小相等,则转动的半径比Ra:Rb=tan37°:tan53°=9:16.
而绳长与半径的关系r=lsinθ,则La:Lb=3:4.故B正确,A、C、D错误.
故选B.
点评:解决本题的关键知道小球圆周运动的向心力的来源,根据牛顿第二定律进行求解.
解答:解:小球所受的合力F合=mgtanθ=mrω2,则角速度的大小ω=
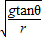 ,
,由于角速度大小相等,则转动的半径比Ra:Rb=tan37°:tan53°=9:16.
而绳长与半径的关系r=lsinθ,则La:Lb=3:4.故B正确,A、C、D错误.
故选B.
点评:解决本题的关键知道小球圆周运动的向心力的来源,根据牛顿第二定律进行求解.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 用一根细绳,一端系住一个质量为m的小球,另一端悬在光滑的水平桌面上方h处,绳长大于h使小球做如图的匀速圆周运动.若使小球不离开桌面,其转速n不得超过
用一根细绳,一端系住一个质量为m的小球,另一端悬在光滑的水平桌面上方h处,绳长大于h使小球做如图的匀速圆周运动.若使小球不离开桌面,其转速n不得超过


 用一根细绳,一端系住一定质量的小球,小球大小忽略.另一端固定在天花板上,使小球做如图的匀速圆周运动.现在有如图5两个这样的装置(a)和(b),(a)、(b)图中,两球转动的角速度大小相同,绳与竖直方向的夹角分别为37°和53°.则a、b两球的转动半径Ra和Rb之比,以及相对应的绳子的长度La和Lb之比分别为:(sin37°=0.6;cos37°=0.8)( )
用一根细绳,一端系住一定质量的小球,小球大小忽略.另一端固定在天花板上,使小球做如图的匀速圆周运动.现在有如图5两个这样的装置(a)和(b),(a)、(b)图中,两球转动的角速度大小相同,绳与竖直方向的夹角分别为37°和53°.则a、b两球的转动半径Ra和Rb之比,以及相对应的绳子的长度La和Lb之比分别为:(sin37°=0.6;cos37°=0.8)( ) 用一根细绳,一端系住一个质量为m的小球,另一端悬在光滑水平桌面上方h处,绳长l大于h,使小球在桌面上做如图所示的匀速圆周运动.若使小球不离开桌面,则小球运动的半径是
用一根细绳,一端系住一个质量为m的小球,另一端悬在光滑水平桌面上方h处,绳长l大于h,使小球在桌面上做如图所示的匀速圆周运动.若使小球不离开桌面,则小球运动的半径是 用一根细绳,一端系住一个质量为m的小球,另一端悬在光滑水平桌面上方h处,绳长l大于h,使小球在桌面上做如图所示的匀速圆周运动.若使小球不离开桌面,其圆周运动的转速最大值是( )
用一根细绳,一端系住一个质量为m的小球,另一端悬在光滑水平桌面上方h处,绳长l大于h,使小球在桌面上做如图所示的匀速圆周运动.若使小球不离开桌面,其圆周运动的转速最大值是( )