题目内容
6.半圆轨道竖直放置,半径R=0.4m,其底端与水平轨道相接,一个质量为m=0.2kg的滑块放在水平轨道C点上,轨道均为光滑,用一个水平的恒力F作用于滑块,使滑块向右运动,当滑块到达半圆轨道的最低点A时撤去F,滑块到达圆的最高点B沿水平方向飞出,恰好落到滑块起始运动的位置C点,则A与C至少应相距多少?这种情况下所需恒力F的大小是多大?(取g=10m/s2)分析 B点的速度最小时,AC距离最小,而B点的最小速度对应最小向心力,等于小球重力;
由动能定理可得拉力F的大小.
解答 解:小球在B点向心力等于重力时,小球在B点的最小:
$mg=m\frac{{v}^{2}}{R}$,
解得:$v=\sqrt{gR}=\sqrt{10×0.4}=2m/s$,
由B到A小球做平抛,可得:
$2R=\frac{1}{2}g{t}^{2}$,
x=vt,
解得:$x=2×\sqrt{\frac{4×0.4}{10}}=0.8m$.
有A到B由动能定理可得:
$Fx-mg2R=\frac{1}{2}m{v}^{2}$,
解得:$F=\frac{\frac{1}{2}×0.2×{2}^{2}+0.2×10×2×0.4}{0.8}=2.5N$.
答:则A与C至少应相距为0.8m;这种情况下所需恒力F的大小是2.5N.
点评 该题突破的关键是以AC的最小距离来确定B点的速度为最小值,结合绳模型可以判定B点的速度,从而顺利打开题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 如国科所示,足够长的平行光滑金属导轨ab、cd与水平面成θ角放置,导轨间距为l,电阻忽略不计,bc端接有电阻R,磁感应强度为B的匀强磁场垂直轨道平面向下.把质量为m、电阻为r的导体棒ef从轨道顶端由静止释放,运动过程中始终与导轨接触良好.则下列说法正确的是( )
如国科所示,足够长的平行光滑金属导轨ab、cd与水平面成θ角放置,导轨间距为l,电阻忽略不计,bc端接有电阻R,磁感应强度为B的匀强磁场垂直轨道平面向下.把质量为m、电阻为r的导体棒ef从轨道顶端由静止释放,运动过程中始终与导轨接触良好.则下列说法正确的是( )
 如国科所示,足够长的平行光滑金属导轨ab、cd与水平面成θ角放置,导轨间距为l,电阻忽略不计,bc端接有电阻R,磁感应强度为B的匀强磁场垂直轨道平面向下.把质量为m、电阻为r的导体棒ef从轨道顶端由静止释放,运动过程中始终与导轨接触良好.则下列说法正确的是( )
如国科所示,足够长的平行光滑金属导轨ab、cd与水平面成θ角放置,导轨间距为l,电阻忽略不计,bc端接有电阻R,磁感应强度为B的匀强磁场垂直轨道平面向下.把质量为m、电阻为r的导体棒ef从轨道顶端由静止释放,运动过程中始终与导轨接触良好.则下列说法正确的是( )| A. | 导体棒做匀加速直线运动 | |
| B. | 通过电阻R的电流与导体棒的速度成反比 | |
| C. | 导体棒减少的重力势能等于回路中产生的热量 | |
| D. | 导体棒运动的最大速度vmin=$\frac{mg(R+r)sinθ}{{B}^{2}{l}^{2}}$ |
18. 如图甲所示,倾角30°、上侧接有R=1Ω的定值电阻的粗糙导轨(导轨电阻忽略不计、且ab与导轨上侧相距足够远),处于垂直导轨平面向上、磁感应强度大小B=1T的匀强磁场中,导轨相距L=1m.一质量m=2kg、阻值r=1Ω的金属棒,在作用于棒中点、沿斜面且平行于导轨的拉力F作用下,由静止开始从ab处沿导轨向上加速运动,棒球运动的速度一位移图象如图乙所示,(b点为位置坐标原点).若金属棒与导轨间动摩擦因数μ=$\frac{\sqrt{3}}{3}$,g=10m/s2,则金属棒从起点b沿导轨向上运动x=1m的过程中( )
如图甲所示,倾角30°、上侧接有R=1Ω的定值电阻的粗糙导轨(导轨电阻忽略不计、且ab与导轨上侧相距足够远),处于垂直导轨平面向上、磁感应强度大小B=1T的匀强磁场中,导轨相距L=1m.一质量m=2kg、阻值r=1Ω的金属棒,在作用于棒中点、沿斜面且平行于导轨的拉力F作用下,由静止开始从ab处沿导轨向上加速运动,棒球运动的速度一位移图象如图乙所示,(b点为位置坐标原点).若金属棒与导轨间动摩擦因数μ=$\frac{\sqrt{3}}{3}$,g=10m/s2,则金属棒从起点b沿导轨向上运动x=1m的过程中( )
 如图甲所示,倾角30°、上侧接有R=1Ω的定值电阻的粗糙导轨(导轨电阻忽略不计、且ab与导轨上侧相距足够远),处于垂直导轨平面向上、磁感应强度大小B=1T的匀强磁场中,导轨相距L=1m.一质量m=2kg、阻值r=1Ω的金属棒,在作用于棒中点、沿斜面且平行于导轨的拉力F作用下,由静止开始从ab处沿导轨向上加速运动,棒球运动的速度一位移图象如图乙所示,(b点为位置坐标原点).若金属棒与导轨间动摩擦因数μ=$\frac{\sqrt{3}}{3}$,g=10m/s2,则金属棒从起点b沿导轨向上运动x=1m的过程中( )
如图甲所示,倾角30°、上侧接有R=1Ω的定值电阻的粗糙导轨(导轨电阻忽略不计、且ab与导轨上侧相距足够远),处于垂直导轨平面向上、磁感应强度大小B=1T的匀强磁场中,导轨相距L=1m.一质量m=2kg、阻值r=1Ω的金属棒,在作用于棒中点、沿斜面且平行于导轨的拉力F作用下,由静止开始从ab处沿导轨向上加速运动,棒球运动的速度一位移图象如图乙所示,(b点为位置坐标原点).若金属棒与导轨间动摩擦因数μ=$\frac{\sqrt{3}}{3}$,g=10m/s2,则金属棒从起点b沿导轨向上运动x=1m的过程中( )| A. | 金属棒做匀加速直线运动 | |
| B. | 金属棒与导轨间因摩擦产生的热量为10J | |
| C. | 通过电阻R的感应电荷量为0.5C | |
| D. | 电阻R产生的焦耳热为0.5J |
16.把一个月牙状的薄板悬挂起来,静止时如图所示.则薄板的重心可能是图中的( )


| A. | A点 | B. | B点 | C. | C点 | D. | D点 |
 如图所示,在倾角θ=30°的绝缘光滑斜面上,固定两根平行光滑金属导轨,间距l=0.4m,下端用阻值R=0.8Ω的电阻连接.质量=0.2kg、电阻r=0.2Ω、长为l的导体杆垂直放置在导轨上,两端与导轨始终接触良好.整个装置放置在垂直于斜面向上的匀强磁场中,磁感应强度B=0.5T.某时刻用平行于导轨向上的推力F作用在杆的中点,使杆从静止开始向上做勻加速直线运动,加速度a=0.5m/s2,2s以后,推力大小恒为0.8N,杆减速运动了0.45m,速度变为0.不计导轨电阻,取g=10m/s2.求:
如图所示,在倾角θ=30°的绝缘光滑斜面上,固定两根平行光滑金属导轨,间距l=0.4m,下端用阻值R=0.8Ω的电阻连接.质量=0.2kg、电阻r=0.2Ω、长为l的导体杆垂直放置在导轨上,两端与导轨始终接触良好.整个装置放置在垂直于斜面向上的匀强磁场中,磁感应强度B=0.5T.某时刻用平行于导轨向上的推力F作用在杆的中点,使杆从静止开始向上做勻加速直线运动,加速度a=0.5m/s2,2s以后,推力大小恒为0.8N,杆减速运动了0.45m,速度变为0.不计导轨电阻,取g=10m/s2.求: 如图所示,U形金属导轨abcd(bc边置于水平面上)的宽L=0.4m,导轨平面与水平面成θ=30°角,质量为m=0.1kg的导体棒PQ放置在导轨上,与bc平行且相距d=0.5m,导体棒与导轨ab、cd接触良好,棒与导轨组成的矩形回路的总电阻R=0.2Ω,整个回路处在匀强磁场中,磁场的磁感应强度随时间变化规律B=2-t(T),规定垂直导轨平面向上为B的正方向.在0-2s内棒PQ始终静止,重力加速度g取10m/s2.求:
如图所示,U形金属导轨abcd(bc边置于水平面上)的宽L=0.4m,导轨平面与水平面成θ=30°角,质量为m=0.1kg的导体棒PQ放置在导轨上,与bc平行且相距d=0.5m,导体棒与导轨ab、cd接触良好,棒与导轨组成的矩形回路的总电阻R=0.2Ω,整个回路处在匀强磁场中,磁场的磁感应强度随时间变化规律B=2-t(T),规定垂直导轨平面向上为B的正方向.在0-2s内棒PQ始终静止,重力加速度g取10m/s2.求:
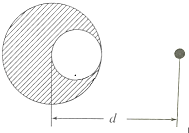 如图所示,在半径为R的铅球中挖出一个球星空穴,空穴与球相切,并通过铅球的球心,在未挖去空穴前铅球质量为M,求有空穴的铅球对与铅球球心距离为d的质量为m的小球的万有引力是多大?
如图所示,在半径为R的铅球中挖出一个球星空穴,空穴与球相切,并通过铅球的球心,在未挖去空穴前铅球质量为M,求有空穴的铅球对与铅球球心距离为d的质量为m的小球的万有引力是多大?