题目内容
 游乐园里的过山车总质量为m,由静止从光滑的倾斜轨道上的P开始下滑,到半径为r的圆形轨道的最高点A时恰好对轨道没有压力.求:
游乐园里的过山车总质量为m,由静止从光滑的倾斜轨道上的P开始下滑,到半径为r的圆形轨道的最高点A时恰好对轨道没有压力.求:(1)过山车在圆形轨道的最高点A时的速度大小;
(2)过山车开始下滑的P距地面的距离为多少.
分析:(1)由题意,过山车通过圆形轨道的最高点A时恰好对轨道没有压力,过山车只受重力,由重力提供向心力,根据牛顿第二定律求解.
(2)过山车从P开始下滑到A的过程,只有重力做功,机械能守恒,根据机械能守恒定律求解.
(2)过山车从P开始下滑到A的过程,只有重力做功,机械能守恒,根据机械能守恒定律求解.
解答:解:(1)在最高点,由题意可知,由重力提供向心力,根据牛顿第二定律有:mg=m
解得:vA=
(2)过山车从P开始下滑到A的过程,由机械能守恒得:mgh=
m
+mg2r
得:h=
r
答:(1)过山车在圆形轨道的最高点A时的速度大小为
;
(2)过山车开始下滑的P距地面的距离为
r.
| ||
| r |
解得:vA=
| gr |
(2)过山车从P开始下滑到A的过程,由机械能守恒得:mgh=
| 1 |
| 2 |
| v | 2 A |
得:h=
| 5 |
| 2 |
答:(1)过山车在圆形轨道的最高点A时的速度大小为
| gr |
(2)过山车开始下滑的P距地面的距离为
| 5 |
| 2 |
点评:对于圆周运动,往往与动能定理、机械能守恒和常见的运动,如平抛运动,竖直运动综合,关键要分析向心力的来源,运用牛顿第二定律和机械能守恒求解.

练习册系列答案
相关题目
 某公园计划修建大型游乐设施“翻滚过山车”,设计轨道总长为842m,每车可载28人.游乐过程中过山车将绕半径为5.5m的大圆环回旋,如图所示.若不考虑一切阻力,取g=10m/s2,求:
某公园计划修建大型游乐设施“翻滚过山车”,设计轨道总长为842m,每车可载28人.游乐过程中过山车将绕半径为5.5m的大圆环回旋,如图所示.若不考虑一切阻力,取g=10m/s2,求: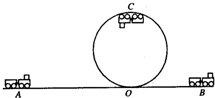 为了测试“过山车”运行过程中的安全性能,生产厂家对空载时的过山车进行了以下试验:让车在P=35kW的恒定功率牵引下,从A点由静止开始沿水平轨道做加速直线运动,经20s到O点时关闭发动机让其冲上半径R=10m的圆形轨道,沿内侧滑行,通过最高点C时的速度恰好是车不脱离轨道的临界速度,最后在右侧的水平轨道滑行至B点停止,设车的总质量m=2t,车在左右水平轨道上所受阻力均是车重的0.1倍,在圆形轨道上所受阻力不计,计算时过山车可看作质点,g取10m/s2.在这次试车中
为了测试“过山车”运行过程中的安全性能,生产厂家对空载时的过山车进行了以下试验:让车在P=35kW的恒定功率牵引下,从A点由静止开始沿水平轨道做加速直线运动,经20s到O点时关闭发动机让其冲上半径R=10m的圆形轨道,沿内侧滑行,通过最高点C时的速度恰好是车不脱离轨道的临界速度,最后在右侧的水平轨道滑行至B点停止,设车的总质量m=2t,车在左右水平轨道上所受阻力均是车重的0.1倍,在圆形轨道上所受阻力不计,计算时过山车可看作质点,g取10m/s2.在这次试车中