Question

【题目】一辆车通过一根跨过定滑轮的轻绳子提升一个质量为m的重物，开始车在滑轮的正下方，绳子的端点离滑轮的距离是H．车由静止开始向左做匀加速运动，经过时间t绳子与水平方向的夹角为θ，如图所示，则（ ）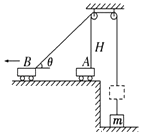

A.车向左运动的加速度的大小为
B.车向左运动的加速度的大小为
C.重物m在t时刻速度的大小为 cosθ?cotθ
D.重物m在t时刻速度的大小为 cotθ

Answer 1

【答案】B,C
【解析】解：AB、小车做匀加速直线运动，根据位移时间关系公式，有： = at2 ，
解得：a= ；故A错误，B正确；
CD、图示时刻小车速度为：v=at= ，
将小车B位置的速度沿着平行绳子和垂直绳子方向正交分解，如图所示：

根据平行四边形定则，有：v1=vcosθ= = cosθcotθ，
其中平行绳子的分速度与重物m的速度相等，故重物速度为 cosθcotθ；故C正确，D错误；
故选：BC．