题目内容
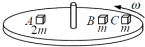
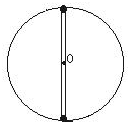
利用双线可以稳固小球在竖直平面内做圆周运动而不易偏离竖直面，如图，用两根长为L的细线系一质量为m的小球，两线上端系于水平横杆上，A、B两点相距也为L，若小球恰能在竖直面内做完整的圆周运动，则小球运动到最低点时，每根线承受的张力为（ ）
A．2
| B．3mg | C．2.5mg | D．
|
小球恰好过最高点时有：mg=m
解得：v1=
①
根据动能定理得，mg?
L=
mv22-
mv12②
由牛顿第二定律得：
T-mg=m
③
联立①②③得，T=2
mg
故A正确，B、C、D错误．
故选：A．
| v12 |
| R |
解得：v1=
|
根据动能定理得，mg?
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
由牛顿第二定律得：
| 3 |
| v22 | ||||
|
联立①②③得，T=2
| 3 |
故A正确，B、C、D错误．
故选：A．
练习册系列答案
名校课堂系列答案
相关题目
