题目内容
20.一辆汽车的质量为10t,在水平路面行驶时发动机的功率和汽车所受阻力都不变,汽车以5m/s 的速度行驶时,加速度为0.75m/s2 ;速度为10m/s时,加速度为0.25m/s2,则发动机的功率为50kW,阻力为2.5×103N,汽车能达到的最大速度为20m/s.分析 根据牛顿第二定律和功率公式P=Fv结合,对两种情况分别列式,求出发动机的功率和阻力大小.当汽车匀速运动时速度最大,由P=Fv和F=f结合求解最大速度.
解答 解:设汽车发动机的功率为P,所受的阻力为f.
根据牛顿第二定律得:
$\frac{P}{{v}_{1}}$-f=ma1;代入得:$\frac{P}{5}$-f=104×0.75 ①
$\frac{P}{{v}_{2}}$-f=ma2;代入得:$\frac{P}{10}$-f=104×0.25 ②
由①②解得 P=5×104W=50kW,f=2.5×103N
当汽车匀速运动时速度最大,此时有牵引力等于阻力,F=f
则最大速度为vm=$\frac{P}{F}$=$\frac{P}{f}$=20m/s
故答案为:50,2.5×103,20.
点评 解决本题的关键要知道发动机的功率是其牵引力的功率,公式P=Fv中,F是牵引力,不是合力.明确汽车的运动过程,知道汽车匀速运动时速度最大.

练习册系列答案
相关题目
10. 如图所示,甲、乙两船在同一条河流中同时开始渡河,M、N分别是甲、乙两船的出发点,两船头与河岸均成α角,甲船船头恰好对准N点的正对岸P点,经过一段时间乙船恰好到达P点,如果划船速度大小相同,且两船相遇,不影响各自的航行,下列判断正确的是( )
如图所示,甲、乙两船在同一条河流中同时开始渡河,M、N分别是甲、乙两船的出发点,两船头与河岸均成α角,甲船船头恰好对准N点的正对岸P点,经过一段时间乙船恰好到达P点,如果划船速度大小相同,且两船相遇,不影响各自的航行,下列判断正确的是( )
 如图所示,甲、乙两船在同一条河流中同时开始渡河,M、N分别是甲、乙两船的出发点,两船头与河岸均成α角,甲船船头恰好对准N点的正对岸P点,经过一段时间乙船恰好到达P点,如果划船速度大小相同,且两船相遇,不影响各自的航行,下列判断正确的是( )
如图所示,甲、乙两船在同一条河流中同时开始渡河,M、N分别是甲、乙两船的出发点,两船头与河岸均成α角,甲船船头恰好对准N点的正对岸P点,经过一段时间乙船恰好到达P点,如果划船速度大小相同,且两船相遇,不影响各自的航行,下列判断正确的是( )| A. | 甲船也能到达正对岸 | B. | 两船渡河时间不相等 | ||
| C. | 两船相遇在NP直线上 | D. | 渡河过程中两船不会相遇 |
1. 如图所示,水平铜盘半径为r,置于磁感应强度为B、方向竖直向下的匀强磁场中,铜盘绕通过圆盘中心的竖直轴以角速度ω做匀速圆周运动,铜盘的边缘及中心处分别通过导线和滑动变阻器R1与理想变压器的原线圈相连,该理想变压器原、副线圈的匝数比为n:1,变压器的副线圈与电阻为R2的负载相连,则( )
如图所示,水平铜盘半径为r,置于磁感应强度为B、方向竖直向下的匀强磁场中,铜盘绕通过圆盘中心的竖直轴以角速度ω做匀速圆周运动,铜盘的边缘及中心处分别通过导线和滑动变阻器R1与理想变压器的原线圈相连,该理想变压器原、副线圈的匝数比为n:1,变压器的副线圈与电阻为R2的负载相连,则( )
 如图所示,水平铜盘半径为r,置于磁感应强度为B、方向竖直向下的匀强磁场中,铜盘绕通过圆盘中心的竖直轴以角速度ω做匀速圆周运动,铜盘的边缘及中心处分别通过导线和滑动变阻器R1与理想变压器的原线圈相连,该理想变压器原、副线圈的匝数比为n:1,变压器的副线圈与电阻为R2的负载相连,则( )
如图所示,水平铜盘半径为r,置于磁感应强度为B、方向竖直向下的匀强磁场中,铜盘绕通过圆盘中心的竖直轴以角速度ω做匀速圆周运动,铜盘的边缘及中心处分别通过导线和滑动变阻器R1与理想变压器的原线圈相连,该理想变压器原、副线圈的匝数比为n:1,变压器的副线圈与电阻为R2的负载相连,则( )| A. | 若R1不变时,变压器原线圈两端的电压为$\frac{1}{2}$Br2ω | |
| B. | 若R1不变时,通过负载R2的电流强度为零 | |
| C. | 若R1不变时,变压器的副线圈磁通量为零 | |
| D. | 若R1变化时,通过R1电流强度为通过负载R2电流的$\frac{1}{n}$ |
8. 如图是街头变压器给用户供电的示意图,此变压器视为理想变压器,输入端接入的电压u=2200$\sqrt{2}$sin100πt(V),输出电压通过输电线输送给用户,输电线的电阻用R表示,理想变压器原、副线圈的匝数比为10:1,题中电表均为理想交流表,则下列说法正确的是( )
如图是街头变压器给用户供电的示意图,此变压器视为理想变压器,输入端接入的电压u=2200$\sqrt{2}$sin100πt(V),输出电压通过输电线输送给用户,输电线的电阻用R表示,理想变压器原、副线圈的匝数比为10:1,题中电表均为理想交流表,则下列说法正确的是( )
 如图是街头变压器给用户供电的示意图,此变压器视为理想变压器,输入端接入的电压u=2200$\sqrt{2}$sin100πt(V),输出电压通过输电线输送给用户,输电线的电阻用R表示,理想变压器原、副线圈的匝数比为10:1,题中电表均为理想交流表,则下列说法正确的是( )
如图是街头变压器给用户供电的示意图,此变压器视为理想变压器,输入端接入的电压u=2200$\sqrt{2}$sin100πt(V),输出电压通过输电线输送给用户,输电线的电阻用R表示,理想变压器原、副线圈的匝数比为10:1,题中电表均为理想交流表,则下列说法正确的是( )| A. | V2表的读数为220$\sqrt{2}$V | |
| B. | A1表的示数随A2表的示数的增大而增大 | |
| C. | 副线圈中交流电的频率为50Hz | |
| D. | 用户端闭合开关S,则V2表读数不变,A1表读数变大,变压器的输入功率增大 |
5.把220V正弦交变电流加在440Ω的电阻上,则( )
| A. | 电压的有效值为220V,电流的有效值为0.5A | |
| B. | 电压的峰值为220V,电流的有效值为0.5A | |
| C. | 电压的有效值为220V,电流的峰值为0.5A | |
| D. | 电压的峰值为220V,电流的最大值为0.5A |
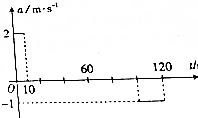 一辆汽车由静止开始沿笔直的公路从甲地运动到乙地,其运动的加速度随时间变化的关系如图,求:
一辆汽车由静止开始沿笔直的公路从甲地运动到乙地,其运动的加速度随时间变化的关系如图,求: