题目内容
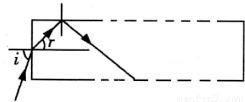
光纤是现代通讯普遍使用的信息传递媒介,它利用全反射原理来传递光信号。现有一根圆柱形光纤,已如制作光纤材料的折射率为n。假设光信号从光纤一端的中心进入。为保证沿任意方向进入的光信号都能传递到另一端,n不能小于某一值。
(1)求n的最小值;
(2)沿不同方向进入光纤的光信号传递到另一端所用的时间会有所不同,求最长与最短时间的比。
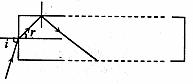
解:⑴设光的入射角为i,折射角为r,根据折射定律得:
![]() ………………………………………⑴
………………………………………⑴
当i趋于90°时,r最大,此时光在侧面的入射角最小,只要能保证此时光在侧面恰好发生全反射,即能保证所有入射光都能发生全反射。即:
![]() ………………………………⑵
………………………………⑵
联立以上两式,并注意到i=90°,可解得:
![]() …………………………………………⑶
…………………………………………⑶
(2)设光从一端垂直入射,不经反射直接到达另一端所用时间为t1,此时所用时间应最短。
设光在光纤中传播速度为v,则:
![]() …………………………………………⑷
…………………………………………⑷
而光经过多次全反射后到达另一端所用时间就会变长,从图中可以看出i越大,发生反射的次数就越多,到达另一端所用时间就越长,当i=90°时,所用时间最长,设为t2,
![]() ..……………………………………⑸
..……………………………………⑸
联立⑴⑷⑸得:![]() …………………⑹
…………………⑹
(1)(2)(5)每式2分,其它各式每式1分。

练习册系列答案
相关题目
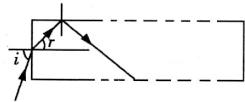 光纤是现代通讯普遍使用的信息传递媒介,它利用全反射原理来传递光信号.现有一根圆柱形光纤,已知制作光纤材料的折射率为n.假设光信号从光纤一端的中心进入.如图所示,为保证沿任意方向进入的光信号都能传递到另一端,n不能小于某一值.
光纤是现代通讯普遍使用的信息传递媒介,它利用全反射原理来传递光信号.现有一根圆柱形光纤,已知制作光纤材料的折射率为n.假设光信号从光纤一端的中心进入.如图所示,为保证沿任意方向进入的光信号都能传递到另一端,n不能小于某一值.