题目内容
13. 一轻质细绳一端系一质量为m=$\frac{1}{20}$kg的小球A,另一端挂在光滑水平轴O上,O到小球的距离为L=0.1m,小球跟水平面接触,但无相互作用,在球的两侧等距离处分别固定一个光滑的斜面和一个挡板,如图所示,水平距离s为2m,现有一小滑块B,质量也为m,从斜面上滑下,与小球碰撞时交换速度,与挡板碰撞不损失机械能,小滑块B与水平面间的动摩擦因数为0.25.若不计空气阻力,并将滑块和小球都视为质点,g取10m/s2,试问:
一轻质细绳一端系一质量为m=$\frac{1}{20}$kg的小球A,另一端挂在光滑水平轴O上,O到小球的距离为L=0.1m,小球跟水平面接触,但无相互作用,在球的两侧等距离处分别固定一个光滑的斜面和一个挡板,如图所示,水平距离s为2m,现有一小滑块B,质量也为m,从斜面上滑下,与小球碰撞时交换速度,与挡板碰撞不损失机械能,小滑块B与水平面间的动摩擦因数为0.25.若不计空气阻力,并将滑块和小球都视为质点,g取10m/s2,试问:(1)若滑块B从斜面某一高度h处滑下与小球第一次碰撞后,使小球恰好在竖直平面内做圆周运动,求此高度h.
(2)若滑块B从h′=5m处滑下,求滑块B与小球第一次碰后瞬间绳子对小球的拉力.
(3)若滑块B从h′=10m处下滑与小球碰撞后,小球在竖直平面内做圆周运动,求小球做完整圆周运动的次数n.
分析 (1)小球恰好在竖直平面内做圆周运动,则在最高点,重力恰好提供向心力;对滑块从下滑到与小球碰撞过程运用动能定律列式;联立方程组求解即可;
(2)先对滑块从下滑到与小球碰撞过程运用动能定律列式求出碰撞前的速度;碰撞,速度传递给小球,然后对小球受力分析,受重力和拉力,合力提供向心力;
(3)滑块B从h=10m 处下滑与小球碰撞后,速度传递给小球,小球在竖直平面内做圆周运动,经过一圈后从左侧碰撞滑块,速度传递给滑块,滑块向右移动,碰撞挡板后返回,再次通过碰撞将速度传递给小球,小球顺时针转动一周,从右侧通过碰撞将速度传递给滑块,滑块向左移动,冲上斜面后返回,再次从左侧碰撞小球,完成一个周期的运动;此后不断重复这个过程,直到小球不能做完整的圆周运动为止
解答 解:(1)小球刚能完成一次完整的圆周运动,它到最高点的速度为v0,在最高点,仅有重力充当向心力,则有
mg=m$\frac{{v}_{0}^{2}}{L}$ ①
在小球从h处运动到最高点的过程中,机械能守恒,
则有mg(h-2L)-μmg$\frac{s}{2}$=$\frac{1}{2}m{v}_{0}^{2}$ ②
解上式有h=0.5m
(2)若滑块从h′=5m处下滑到将要与小球碰撞时速度为v1,则有mgh′-$μmg•\frac{S}{2}$=$\frac{1}{2}m{v}_{1}^{2}$ ③
滑块与小球碰后的瞬间,同理滑块静止,小球以的速度开始作圆周运动,绳的拉力T和重力的合力充当向心力,则有 T-mg=m$\frac{{v}_{1}^{2}}{L}$ ④
解得
T=48N
(3)小球恰好能做完整的圆周运动,机械能为:E=$\frac{1}{2}$mv${\;}_{0}^{2}$+mg•2L
滑块和小球第一次碰撞后,每在平面上经s路程后再次碰撞,即机械能损失为:△E损=f•S=μmgS,则根据能量守恒定律,有$\frac{mgh′-μmg•\frac{S}{2}-\frac{1}{2}m{v}_{0}^{2}-2mgL}{μmgS}+1$≥n
解得:n=20次
即小球做完整圆周运动的次数n为20
答:(1)若滑块B从斜面某一高度h=0.5m处滑下与小球第一次碰撞后,使小球恰好在竖直平面内做圆周运动;
(2)若滑块B从h′=5m处滑下,滑块B与小球第一次碰后瞬间绳子对小球的拉力为48N.
(3)若滑块B从h′=10m处下滑与小球碰撞后,小球在竖直平面内做圆周运动,小球做完整圆周运动的次数n为20.
点评 本题关键是要明确小球和滑块的运动的全部过程,然后根据机械能守恒定律和能量守恒定律以及动能定理列式求解,注意机械能的损失等于摩擦力做功.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 据《天文学与天体物理学》报道,在地球的北半球就可以观测到距离地球1.3万光年的鹿豹座星团中两颗恒星,如图所示,它是由两颗大质量恒星构成的双星系统.该系统的两颗恒星质量分别为太阳的38倍和32倍,轨道周期为28小时,现两恒星外表面已开始接触,若已知太阳质量,引力常量,两星体可视为质量分布均匀的球体,则( )
据《天文学与天体物理学》报道,在地球的北半球就可以观测到距离地球1.3万光年的鹿豹座星团中两颗恒星,如图所示,它是由两颗大质量恒星构成的双星系统.该系统的两颗恒星质量分别为太阳的38倍和32倍,轨道周期为28小时,现两恒星外表面已开始接触,若已知太阳质量,引力常量,两星体可视为质量分布均匀的球体,则( )| A. | 可求出两星球球心之间的距离 | |
| B. | 不可能求出两星球中任何一个的半径 | |
| C. | 可求出两星球中任何一个的密度 | |
| D. | 不可能求出两星球中任何一个的线速度 |
 如图所示,斜面上有a、b、c、d 四个点,ab=bc=cd,从a点以初速度v0水平抛出一个小球,它恰好落在斜面上的b点;若小球以初速度2v0水平抛出,不计空气阻力,则下列判断正确的是( )
如图所示,斜面上有a、b、c、d 四个点,ab=bc=cd,从a点以初速度v0水平抛出一个小球,它恰好落在斜面上的b点;若小球以初速度2v0水平抛出,不计空气阻力,则下列判断正确的是( )| A. | 小球一定落在c点 | |
| B. | 小球可能落在b点与c点之间 | |
| C. | 小球落在斜面的速度方向与斜面的夹角一定相同 | |
| D. | 小球落在斜面的速度方向与斜面的夹角一定变大 |

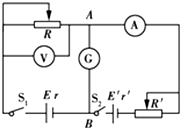 采用伏安法测量电源电动势E和内阻r时,由于电表因素带来了实验的系统误差.某研究性学习小组对此实验进行改进,设计出如图所示的测量电源电动势E和内电阻r的电路,E′是辅助电源,A、B两点间有一灵敏电流计G.
采用伏安法测量电源电动势E和内阻r时,由于电表因素带来了实验的系统误差.某研究性学习小组对此实验进行改进,设计出如图所示的测量电源电动势E和内电阻r的电路,E′是辅助电源,A、B两点间有一灵敏电流计G. 如图所示,行车通过长为5米的吊臂,吊着质量为1吨的钢材,以v=2m/s速度沿水平方向匀速行驶,行车突然停车,问:
如图所示,行车通过长为5米的吊臂,吊着质量为1吨的钢材,以v=2m/s速度沿水平方向匀速行驶,行车突然停车,问: 如图所示,在竖直平面内的平面直角坐标系xOy,在y轴右边有水平向左的匀强电场,在y轴左边有竖直向上的匀强电场(水平和竖直两个匀强电场的场强大小相等)和垂直于纸面向外的匀强磁场(图中未画出).一质量为m,电荷量为+q的微粒从点P(L,0)由静止释放后沿PQ运动,当微粒进入第三象限后微粒做匀速圆周运动,且与x轴只有一个交点,求:
如图所示,在竖直平面内的平面直角坐标系xOy,在y轴右边有水平向左的匀强电场,在y轴左边有竖直向上的匀强电场(水平和竖直两个匀强电场的场强大小相等)和垂直于纸面向外的匀强磁场(图中未画出).一质量为m,电荷量为+q的微粒从点P(L,0)由静止释放后沿PQ运动,当微粒进入第三象限后微粒做匀速圆周运动,且与x轴只有一个交点,求: 某兴趣小组的实验装置如图1所示,通过电磁铁控制的小球从A点自由下落,下落过程中经过光电门B时,通过与之相连的毫秒计时器(图中未画出)记录下挡光时间t,测出A、B之间的距离h.实验前应调整光电门位置使小球下落过程中球心通过光电门中的激光束.
某兴趣小组的实验装置如图1所示,通过电磁铁控制的小球从A点自由下落,下落过程中经过光电门B时,通过与之相连的毫秒计时器(图中未画出)记录下挡光时间t,测出A、B之间的距离h.实验前应调整光电门位置使小球下落过程中球心通过光电门中的激光束.