题目内容
嫦娥一号”的成功发射,为实现中华民族几千年的奔月梦想迈出了重要的一步.已知“嫦娥一号”绕月飞行轨道近似 为 圆形,距月球表面高度为 H,飞行周期为 T,月球的半径为 R,引力常量为 G.求:(1)“嫦娥一号”绕月飞行时 的线速度大小;
(2)月球的质量;
(3)若发射一颗绕月球表面做匀速圆周运动的飞船,则其绕月运行的线速度应为多大.
【答案】分析:“嫦娥一号”的轨道半径r=R+H,由v=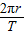 求解线速度.根据月球对“嫦娥一号”的万有引力提供“嫦娥一号”的向心力,列方程求解月球的质量.绕月球表面做匀速圆周运动的飞船轨道半径约R.
求解线速度.根据月球对“嫦娥一号”的万有引力提供“嫦娥一号”的向心力,列方程求解月球的质量.绕月球表面做匀速圆周运动的飞船轨道半径约R.
解答:解:(1)“嫦娥一号”绕月飞行时 的线速度大小v=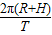
(2)设月球质量为M,“嫦娥一号”的质量为m,根据牛顿第二定律得
G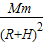 =
=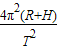
解得M=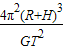 .
.
(2)设绕月飞船运行的线速度为V,飞船质量为m,则
G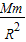 =
=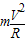
又M=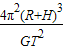 ,联立解得V=
,联立解得V=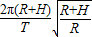 .
.
答:(1)“嫦娥一号”绕月飞行时的线速度大小为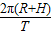 ;
;
(2)月球的质量为M=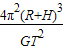 ;
;
(3)若发射一颗绕月球表面做匀速圆周运动的飞船,则其绕月运行的线速度应为=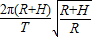 .
.
点评:本题考查应用万有引力定律解决实际问题的能力,关键要建立模型,理清思路.
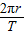 求解线速度.根据月球对“嫦娥一号”的万有引力提供“嫦娥一号”的向心力,列方程求解月球的质量.绕月球表面做匀速圆周运动的飞船轨道半径约R.
求解线速度.根据月球对“嫦娥一号”的万有引力提供“嫦娥一号”的向心力,列方程求解月球的质量.绕月球表面做匀速圆周运动的飞船轨道半径约R.解答:解:(1)“嫦娥一号”绕月飞行时 的线速度大小v=
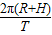
(2)设月球质量为M,“嫦娥一号”的质量为m,根据牛顿第二定律得
G
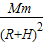 =
=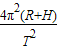
解得M=
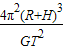 .
.(2)设绕月飞船运行的线速度为V,飞船质量为m,则
G
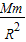 =
=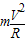
又M=
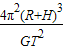 ,联立解得V=
,联立解得V=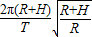 .
.答:(1)“嫦娥一号”绕月飞行时的线速度大小为
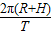 ;
; (2)月球的质量为M=
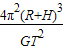 ;
; (3)若发射一颗绕月球表面做匀速圆周运动的飞船,则其绕月运行的线速度应为=
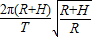 .
.点评:本题考查应用万有引力定律解决实际问题的能力,关键要建立模型,理清思路.

练习册系列答案
相关题目