题目内容
9. 如图所示,直角玻璃三棱镜置于空气中,已知∠A=60°,∠C=90°,一束极细的光于AC的中点D垂直AC面入射,AD=a,棱镜的折射率为n=$\sqrt{2}$.
如图所示,直角玻璃三棱镜置于空气中,已知∠A=60°,∠C=90°,一束极细的光于AC的中点D垂直AC面入射,AD=a,棱镜的折射率为n=$\sqrt{2}$.(1)求此玻璃对空气的临界角;
(2)光从棱镜第一次射入空气时的折射角.
分析 (1)根据全反射临界角公式sinC=$\frac{1}{n}$求临界角C.
(2)画出光路图,判断光线在AB面和BC面上能否发生全反射,由几何知识求出光线第一次射入空气时的入射角,由折射定律求解折射角.
解答  解:(1)设玻璃对空气的临界角为C,
解:(1)设玻璃对空气的临界角为C,
则$sinC=\frac{1}{n}=\frac{{\sqrt{2}}}{2}$,所以C=45°.
(2)如图所示 因为i1=60°>C,所以光线在AB面上将发生全反射.
由几何知识得:i2=i1-30°=30°<C,则光线从BC面上第一次射入空气.
由折射定律有:$\frac{sinr}{{sin{i_2}}}=\sqrt{2}$
得 r=45°
答:
(1)此玻璃的临界角是45°.
(2)光从棱镜第一次射入空气时的折射角是45°.
点评 本题是几何光学问题,做这类题目,一般首先要正确画出光路图,当光线从介质射入空气时要考虑能否发生全反射,要能灵活运用几何知识帮助我们分析角的大小.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20. 如图所示,一质点从A点开始向C点做匀加速直线运动,它在时间T内通过位移x1到达B点,接着又在时间T内通过位移x2到达C点.以下判断正确的是( )
如图所示,一质点从A点开始向C点做匀加速直线运动,它在时间T内通过位移x1到达B点,接着又在时间T内通过位移x2到达C点.以下判断正确的是( )
 如图所示,一质点从A点开始向C点做匀加速直线运动,它在时间T内通过位移x1到达B点,接着又在时间T内通过位移x2到达C点.以下判断正确的是( )
如图所示,一质点从A点开始向C点做匀加速直线运动,它在时间T内通过位移x1到达B点,接着又在时间T内通过位移x2到达C点.以下判断正确的是( )| A. | 物体在A点的速度一定为0 | |
| B. | 物体在B点的速度大小为$\frac{{{x_1}+{x_2}}}{2T}$ | |
| C. | 物体运动的加速度大小为$\frac{{{x_2}-{x_1}}}{{4{T^2}}}$ | |
| D. | 物体运动的加速度大小为$\frac{{{x_2}-{x_1}}}{T^2}$ |
17.两根磁铁放在两辆小车上,小车能在水平面上自由移动,甲车与磁铁总质量为1kg,乙车与磁铁总质量为2kg,两根磁铁的S极相对,推动一下使两车相向而行,若某时刻甲的速度为3m/s,乙的速度为2m/s,可以看到,他们还没有碰上就分开了,则( )
| A. | 甲车开始反向时,乙车速度减为0.5m/s,方向不变 | |
| B. | 乙车开始反向时,甲车速度减为0.5m/s,方向与原来方向相反 | |
| C. | 两车距离最近时,速率相等,方向相反 | |
| D. | 两车距离最近时,速度都为0.33m/s,方向都与乙车原来的速度方向一致 |
4.1897年英国物理学家汤姆孙发现了电子,被称为“电子之父”,下列关于电子的说法正确的是( )
| A. | 汤姆孙通过阴极射线在电场和磁场中的运动得出了阴极射线是带负电的粒子的结论,并求出了阴极射线的比荷 | |
| B. | 汤姆孙通过对光电效应的研究,发现了电子 | |
| C. | 电子的质量无法测定 | |
| D. | 汤姆孙通过对不同材料的阴极发出的射线的研究,并研究了光电效应等现象,说明电子是原子的组成部分,是比原子更基本的物质单元 |
14.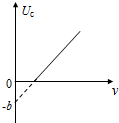 在某次光电效应实验中,得到的遏制电压Uc与入射光的频率ν的关系如图所示,若该直线的斜率和纵截距分别为k和-b,电子电荷量的绝对值为e,则( )
在某次光电效应实验中,得到的遏制电压Uc与入射光的频率ν的关系如图所示,若该直线的斜率和纵截距分别为k和-b,电子电荷量的绝对值为e,则( )
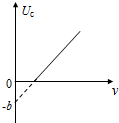 在某次光电效应实验中,得到的遏制电压Uc与入射光的频率ν的关系如图所示,若该直线的斜率和纵截距分别为k和-b,电子电荷量的绝对值为e,则( )
在某次光电效应实验中,得到的遏制电压Uc与入射光的频率ν的关系如图所示,若该直线的斜率和纵截距分别为k和-b,电子电荷量的绝对值为e,则( )| A. | 普朗克常量可表示为ek | |
| B. | b由入射光决定,与所用材料无关 | |
| C. | 所用材料的逸出功可表示为eb | |
| D. | 若更换材料再实验,得到的图线的k和b都要改变 |
3.关于电场强度E的说法正确的是( )
| A. | 电场中某点的场强方向跟正电荷在该点所受的电场力的方向相同 | |
| B. | 根据E=$\frac{F}{q}$可知,电场中某点的电场强度与电场力F成正比,与电量q成反比 | |
| C. | 是矢量,与F的方向一致 | |
| D. | 在点电荷Q附近任意一点,若没有把试探电荷q放进去,则这一点的电场强度为零 |
20.将一个物体以速度v水平抛出,当物体的竖直速度与水平速度的大小相等时,所经历的时间为( )
| A. | $\frac{v}{g}$ | B. | $\frac{v}{2g}$ | C. | $\frac{2v}{g}$ | D. | $\frac{{\sqrt{2}v}}{g}$ |

